The aim is to calculate as approximately as possible, what is the empty volume of the interior of a double closure of cylindrical containers in order to be able to estimate the maximum volume of rubber that we should put in a lid, without damaging the formation of the closure, and can maintain the tightness of the container.
We will use the fastener dimensions indicated in the SEFEL Recommendation Nº1 (1999) and within these, a nominal tightening value and a tightening value at the upper limit (very tight), which will allow us to define the working tolerance for the rubberising process.
All measurements will be represented in millimeters, so the volume will be established in mm3.
The mathematical model that is established is approximate, since it will not always be a perfect ellipse, depending on the characteristics of the metal and the profiles of the rollers used.
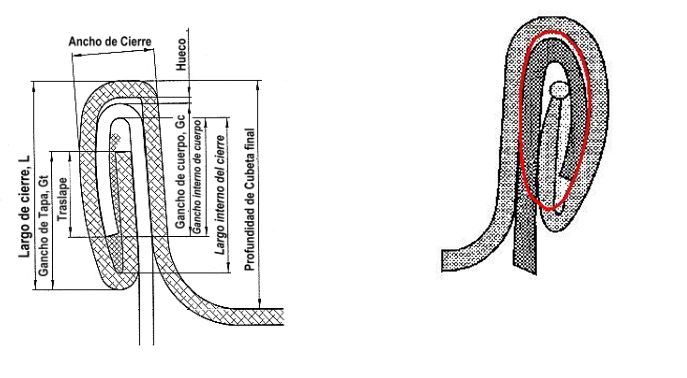
SURFACE OF THE SEAL SECTION
For practical purposes we consider the closure section as an ellipse. For a more precise calculation, we consider only the ellipse of the interior, so that the exterior material left over from the lid does not intervene. This could be represented as follows:
In this inner ellipse, we must calculate the area of the entire marked section:
Where L=Length of the ellipse, and is equal to the length of the closure minus twice the thickness of the lid, and E the width of the ellipse, equal to the width of the closure, also minus twice the thickness of the lid.
According to this, the above formula would be as follows:
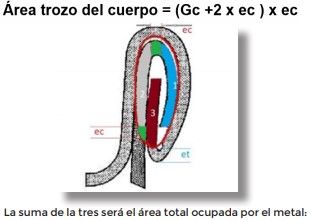
We then calculate the area occupied by the metal inside the ellipse. This area is composed of three segments: two corresponding to the body and one to the lid.
The two hooks (body and lid) and a third segment formed by the body and the upper curve of the same.
We determine the area of each one of them:
1 The body hook, slightly curved, let’s consider it as its length, and a correction factor of 10% for the curvature. Your area would be:
2 The cover hook does not fit in whole, but the part that remains outside corresponds to a length equal to the thickness of the material. Therefore, your area would be:
3 The piece of the body that enters inside the internal ellipse of the fastener is considered as a length equal to Gc but it also has a correction, corresponding to the curve and the excess of its length, that enters inside the ellipse so we can consider that it corresponds to its length plus two thicknesses of metal, one for the excess and one for the hook curve: Thus:
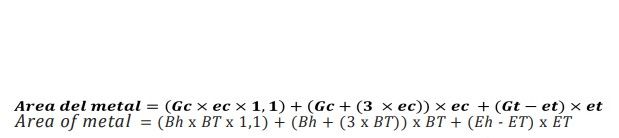
Equation 3
Therefore, the free area of the section of the ellipse above is equal to the subtraction of equations 2 and 3. Let’s see a practical example, for a container of diameter 73 (# 300) with a characteristic closure within the SEFEL I dimensions:
Length: 2,80 G. Body: 1,85
Width: 1,05 G. Cover: 1,90
ec = 0.16 Overlap: 1.1
et = 0,20 %Compactness 87%.
For a closure of given dimensions, the surface of the inner ellipse would be:
Area = ((2,80 – 0,40) / 2) x ((1,05-0,40) / 2) x π =1,225 mm2 Metal surface: (1,85×0,16×1,1) + (1,85+0,48) x 0,16 +(1,70x,20) = 1,013 mm2
Free area = 1,225 -1,013 = 0,212 mm2
VOLUME OF THE INNER ELLIPSOID OF THE CLOSURE, AND FREE VOLUME
If we consider this surface for the thickness of 1 mm, we will have the volume of the cylindroid of 1 mm height. Considering the complete development of the closure, whose length we calculate as the diameter of the centre of the closure section, multiplied by pi, we will have a simple mathematical model of the volume of the complete closure. Thus, for a container of nominal diameter 73, the closure will have an average diameter of 74 mm. The length of the closure development, therefore, will be
Length of the lock development =74 x π = 232.48 mm
Continuing with the previous example, the volume calculated for the inside of the closure would be:
0.212 x 232.48 = 49.3 mm3 to occupy 100 % of the empty volume.
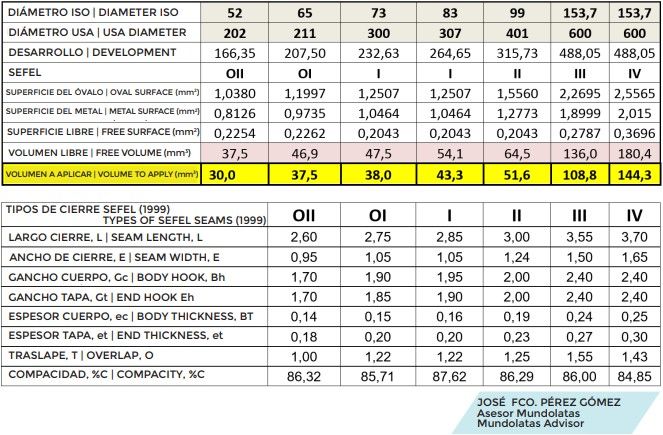
We can establish the sealing values for the different diameters, according to SEFEL values, with a degree of tightening according to the standard and for tighter values, thus calculating the minimum volume of rubber necessary for a seal.
APPLICATION VOLUME
As a general term, we can calculate the volume to be occupied by the rubber as 80% of the maximum volume we have. To calculate the weights, we only have to multiply this volume by the density of the dry rubber, applying the tolerance recommended by the supplier.















0 Comments