Se pretende calcular de forma lo más aproximada posible, cual es el volumen vacío del interior de un doble cierre de envases cilíndricos para, de esta forma, poder estimar cual es el volumen máximo de goma que deberíamos poner en una tapa, sin que perjudique a la formación del cierre, y pueda mantener la estanqueidad del envase.
Utilizaremos las dimensiones de cierres indicadas en la Recomendación SEFEL Nº1 (1999) y dentro de éstas, un valor de apriete nominal y un valor de apriete al límite superior (muy apretado), que nos permita definir la tolerancia de trabajo para el proceso de engomado.
Todas las medidas se van a representar en milímetros, por lo que el volumen quedará establecido en mm3.
El modelo matemático que se establece es aproximado, ya que no siempre será una elipse perfecta, en función de las características del metal y los perfiles de las rulinas empleadas.
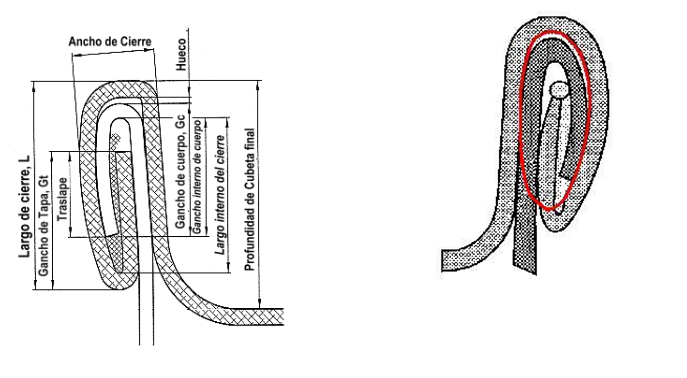
SUPERFICIE DE LA SECCIÓN DEL CIERRE
A efectos prácticos consideramos la sección del cierre como una elipse. Para una mayor precisión del cálculo, consideramos solo la elipse del interior, de forma que no intervenga el material exterior sobrante de la tapa. Esto podría quedar representado de la siguiente forma:
En esta elipse interna, debemos calcular el área de toda la sección marcada:
Donde L=Largo de la elipse, y es igual a la longitud del cierre menos dos veces el espesor de la tapa, y E el ancho de la elipse, igual al ancho del cierre, también menos dos veces el espesor de la tapa.
egún esto, la formula anterior quedaría como sigue:
Calculamos a continuación, el área ocupada por el metal, dentro de dicha elipse. Esta área, está compuesta por tres segmentos: dos correspondientes al cuerpo y uno a la tapa.
Los dos ganchos (cuerpo y tapa) y un tercer segmento formado por el cuerpo y la curva superior del mismo.
Determinamos pues el área de cada uno de ellos:
1 El gancho de cuerpo, ligeramente curvo, lo consideremos como su longitud, y un factor de corrección del 10% por la curvatura. Su área seria:
2 El gancho de tapa, no entra entero, pero la parte que queda fuera se corresponde a una longitud igual al espesor del material. Por tanto, su área sería:
3 El trozo del cuerpo que entra dentro de la elipse interna del cierre se considera como una longitud igual al Gc pero tiene también una corrección, correspondiente a la curva y al excedente de su longitud, que entra dentro de la elipse por lo que podemos considerar que se corresponde a su longitud más dos espesores de metal, una por el excedente y una por la curva del gancho: Así:
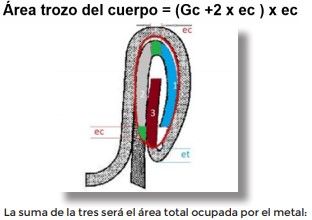
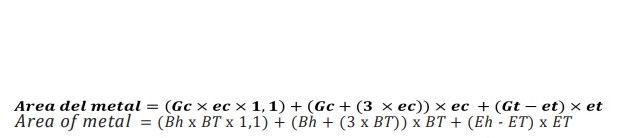
Ecuación 3
Por lo tanto, la superficie libre de la sección de la elipse anterior es igual a la resta de las ecuaciones 2 y 3. Veamos un ejemplo práctico, para un envase de diámetro 73 (# 300) con un cierre característico dentro de las dimensiones SEFEL I:
Largo: 2,80 G. Cuerpo: 1,85
Ancho: 1,05 G. Tapa: 1,90
ec = 0,16 Traslape: 1,1
et = 0,20 %Compacidad 87%
Para un cierre de dimensiones indicadas, la superficie de la elipse interna sería:
Área = ((2,80 – 0,40) / 2) x ((1,05-0,40) / 2) x π =1,225 mm2 Superficie del metal: (1,85×0,16×1,1) + (1,85+0,48) x 0,16 +(1,70x,20) = 1,013 mm2
Superficie libre = 1,225 –1,013 = 0,212 mm2
VOLUMEN DEL ELIPSOIDE INTERIOR DEL CIERRE, Y VOLUMEN LIBRE
Si consideramos esta superficie para el grueso de 1 mm, tendremos el volumen del cilindroide de 1 mm de altura. Considerando el desarrollo completo del cierre, cuya longitud calculamos como el diámetro del centro de la sección del cierre, multiplicado por pi, tendremos un modelo matemático sencillo del volumen del cierre completo. Así, para un envase de diámetro nominal 73, el cierre tendrá un diámetro medio de 74 mm. La longitud del desarrollo del cierre, será, por tanto
Longitud del desarrollo del cierre =74 x π = 232,48 mm
Continuando con el ejemplo anterior, el volumen calculado para el interior del cierre sería:
0,212 x 232,48 = 49,3 mm3 para ocupar el 100 % del volumen vacío.
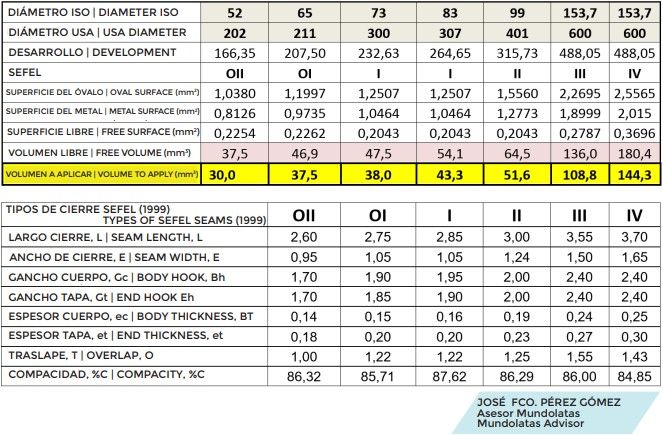
Podemos establecer los valores de cierre para los diferentes diámetros, de acuerdo con los valores SEFEL, con un grado de apriete según la norma y para valores más apretados, calculando así, el volumen mínimo de goma necesario para un cierre.
VOLUMEN A APLICAR
Como término general, podemos calcular el volumen a ocupar por la goma como el 80% del volumen máximo que tenemos. Para calcular los pesos, solo tendremos que multiplicar dicho volumen por la densidad de la goma seca, aplicando la tolerancia recomendada por el proveedor.













0 comentarios