它旨在尽可能粗略地计算出圆柱形容器的双盖内部的空体积，以便以此方式估算出我们应该放入盖子的最大橡胶体积，不会损害封盖的形成，并且可以保持容器的密封性。

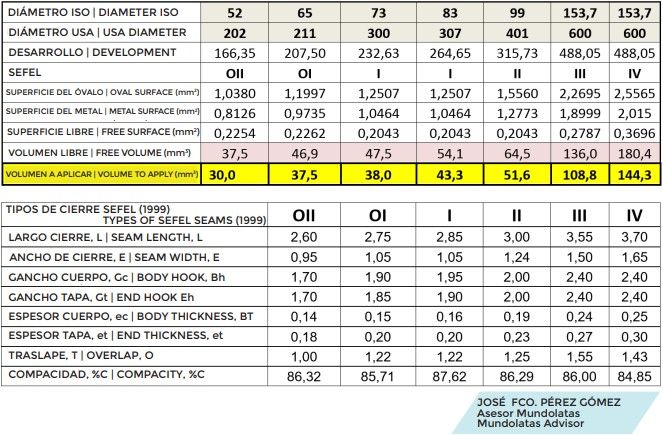
我们将使用SEFEL建议1（1999）中指示的密封件尺寸，在这些尺寸中，标称扭矩值和上限扭矩值（非常紧密），这使我们能够定义上胶的工作公差过程。

所有尺寸均以毫米为单位，因此体积将以毫米为单位³ 。

建立的数学模型是近似的，因为它不一定总是理想的椭圆形，具体取决于金属的特性和所用辊的外形。

据此，以前的公式如下：

然后，我们计算所述椭圆内金属所占的面积。 该区域由三部分组成：两部分对应于主体，另一部分对应于盖子。

两个钩（主体和盖）和由主体和上部弯曲形成的第三段。

因此，我们确定每个区域：

1个略微弯曲的车身挂钩将其视为其长度，并且曲率的校正系数为10％。 您的区域将是：

二盖钩并没有完全移开，但留在外部的部分的长度等于材料的厚度。 因此，其面积为：

3 进入闭合的内部椭圆内的那部分物体被认为是等于Gc的长度，但也有一个修正，对应于进入椭圆内的曲线及其长度的超出部分，因此我们可以认为对应于其长度加上两种金属厚度，一种代表多余的厚度，另一种代表弯钩的曲线：因此：

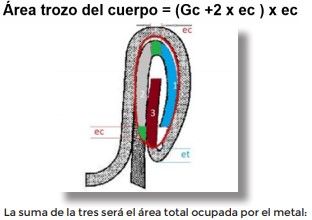
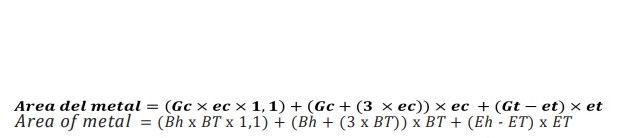
方程式3

因此，先前椭圆的截面的自由表面等于方程式2和3的减法。 让我们看一个实际的示例，该容器的直径为73（＃300），并且在SEFEL I尺寸内具有特征性的闭合：

长度：2.80克。身体：1.85

宽度：1.05克。盖：1.90

ec = 0.16重叠：1.1

et = 0.20％紧密度87％

对于指定尺寸的闭合，内部椭圆的表面为：

面积=（（2.80-0.40）/ 2）x（（1.05-0.40）/ 2）x π = 1,225平方毫米金属表面：（1.85×0.16×1.1）+（1.85 + 0.48）x 0.16 +（1.70x，20）= 1.013平方毫米

自由表面= 1,225 –1,013 = 0,212平方毫米

封闭层的内部椭圆体的体积和自由体积

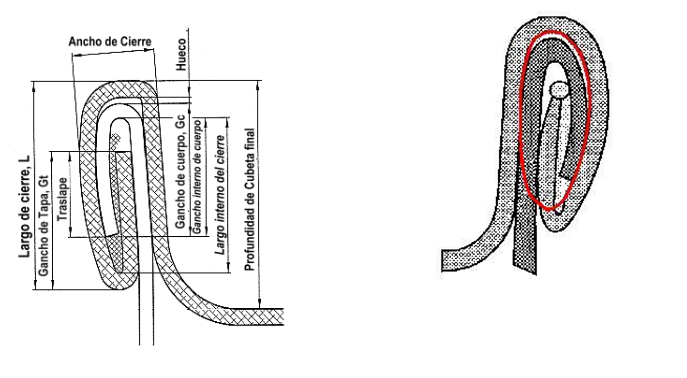
如果我们认为此表面的厚度为1毫米，那么圆柱体的体积将为1毫米高。 考虑到封闭件的完整发展，我们将其长度计算为封闭件截面中心的直径乘以pi，我们将得到一个完整封闭件体积的简单数学模型。 因此，对于标称直径为73的容器，封盖的平均直径为74毫米。 因此，接缝展开的长度将为

接缝展开的长度= 74 x π = 232.48毫米

继续前面的示例，为封闭件内部计算的体积为：

0.212 x 232.48 = 49.3 mm3占空隙体积的100％ 。

我们可以根据SEFEL值确定不同直径的密封值，并根据标准和更紧的值确定拧紧程度，从而计算出密封所需的最小橡胶量。

申请数量

一般而言，我们可以将橡胶所占的体积计算为最大体积的80％。 要计算重量，我们仅需使用供应商建议的公差，将该体积乘以干橡胶的密度即可。