Vamos definir de uma forma muito simples cada um dos conceitos básicos utilizados num sistema de controlo de qualidade por variáveis aplicadas na inspecção de contentores.

Primeiro vamos definir o que queremos dizer por variáveis.

QUE TIPOS DE VARIÁVEIS CONHECEMOS?
Há dois tipos de variáveis a considerar: Variáveis Contínuas e Variáveis Discretas.

Variáveis contínuas
As variáveis contínuas são aquelas que são medidas.
Variáveis discretas
variáveis discretas são contadas.
Os primeiros dão origem ao controlo por variáveis e os segundos ao controlo por atributos.

As características de qualidade que vamos chamar variáveis são todas aquelas que podem ser representadas por um número. Por exemplo, o tamanho de um parafuso, a resistência das resistências dos fios, o teor de cinzas em carbono, etc., etc., etc.
Os atributos são aquelas características de qualidade não mensuráveis, cuja dimensão geralmente não pode ser representada por um número. Como por exemplo, podemos considerar imperfeições visuais das superfícies dos produtos, tais como manchas, diferenças de tom, aspectos de uma solda, etc., etc., etc.
Finalmente, devemos levar em conta que tanto os processos quanto os lotes acabados podem ser inspecionados por atributos ou por variáveis.

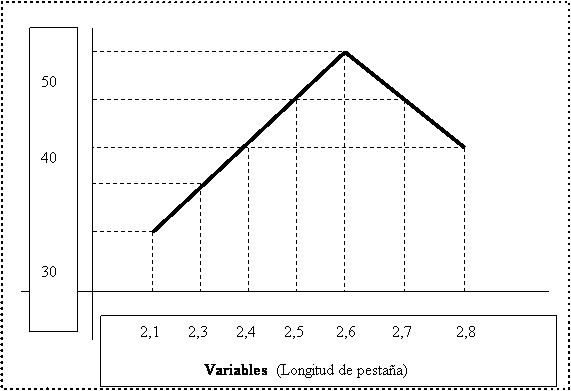
A melhor maneira é usar um exemplo prático. Suponhamos que estamos a controlar o comprimento da flange do corpo do contentor. Após uma série de medições, fazemos um gráfico com elas, como mostra a figura nº 1. Tomamos no eixo das abcissas os valores encontrados para os comprimentos dos flanges e na ordenada o número de recipientes.

Com este gráfico em vista, vamos definir como:

Variável: O parâmetro a ser medido. Neste caso, o comprimento da pestana.

Frequência: Número de vezes que uma variável é repetida. No nosso exemplo, o número de contentores.

Caminho: O intervalo sobre o qual uma variável se move. Entre 2,1 e 2,8 mm (Valores de Comprimento do Flange)

Intervalo: Um agrupamento de valores de uma variável dentro de um determinado intervalo. Por exemplo: agrupamento de todos os valores entre 2,3 e 2,4 no valor 2,4.

Amplitude: Diferença entre os valores extremos do caminho. No nosso exemplo das abas: 2,8 – 2,1 = 0,7 amplitude.

Média: (ou média aritmética): Soma de todos os valores dividida pelo número total de dados.

X = (10*2.1 + 20*2.3 + 30*2.4 + 40*2.5 + 50*2.6 + 40*2.7 + 30*2.8) / (10 + 20 + 30 + 40 + 50 + 40 + 30 ) = ( 21 + 46 + 72 + 100 + 130 + 108 + 84) / 220 = 2.55

Mediana: O valor da distribuição, assumido como ordenado da menor para a maior, que tem o mesmo número de frequências à sua esquerda e à sua direita, ou seja, o valor que ocupa o lugar central, assumindo um número ímpar de dados. Se o número de dados for igual, pode-se dizer que existem dois valores medianos e a média aritmética é tomada entre eles.

Continuando com o exemplo anterior do comprimento das pestanas que teríamos:

Frequências = 10 + 20 + 30 + 40 + 50 + 40 + 40 + 30 = 220

220 seria a frequência absoluta ou cumulativa

Frequência central = 220 / 2 = 110

Portanto, a mediana seria:
2.6
Uma vez que este é o valor da variável que ocupa o 110º lugar desde o início.

Variável de Frequência Cumulativa (m/m)

10 10 2,1

20 30 2,3

30 60 2,4

40 100 2,5

50 150 2,6

40 190 2,7

30 220 2,8

Mais informações em:

http://html.rincondelvago.com/control-de-calidad-estadistico.html

Voltar ao Can World Control