Poiché è considerato di interesse, è sviluppato in questo lavoro, il modo di calcolare la geometria del profilo di taglio a zigzag di fogli e strisce di banda stagnata destinati alla fabbricazione di fondi.

INTRODUZIONE

Nella seconda metà del secolo scorso, la necessità di ridurre i costi ha gradualmente implementato l’imperativo di sfruttare al massimo la superficie metallica dedicata alla fabbricazione di tappi e fondi. A questo scopo, il taglio a zig-zag è stato introdotto per la prima volta nelle bobine di stampa, e più tardi la stessa tecnica è stata usata per tagliare i fogli dalle bobine.

Lo scopo di questo articolo è di presentare le nozioni di base per il calcolo della silhouette, o profilo, di questi tagli a zig-zag. In spagnolo, per designare questo tipo di tosatura, si è diffuso l’uso della parola inglese “scroll shearing”. Pertanto, d’ora in poi useremo questo termine. Chiameremo taglio a rotolo primario quello fatto sulle linee di taglio delle bobine, e taglio a rotolo secondario quello fatto sulle cesoie per la preparazione di strisce o nastri per le presse.

Sebbene le strisce siano a volte usate per stampi singoli – punzone singolo – e quindi contengono solo una fila di fondi, il caso più usuale è per stampi doppi, cioè strisce a doppia fila. Questo studio si concentrerà quindi su quest’ultimo tipo.

IMPOSTAZIONI INIZIALI

Per iniziare il calcolo, dobbiamo conoscere alcuni dati in anticipo. Questi sono:

– D = Il diametro di taglio del materiale necessario per fustellare il coperchio. Deve essere stato precedentemente calcolato e verificato praticamente.

– N1 = Numero di tagli da ottenere per banda. Saremo limitati da:

– il passo di taglio massimo/minimo della linea di taglio delle bobine.

– la larghezza massima/minima del foglio consentita dalla cesoia a scorrimento.

– la lunghezza massima/minima della striscia che la macchina accetta.

Questi dati saranno indicati nei manuali delle macchine.

– N2 = Numero di bande che vogliamo ottenere per foglio. Sarà limitato da:

– la massima larghezza/minuto della bobina che la linea di taglio può gestire.

– la lunghezza massima/minima del foglio che la cesoia a scorrimento può gestire.

– F1 = Taglio minimo tra i tagli.

– F2 = Rifilatura tra il taglio e il bordo laterale della banda

– F3 = Trim tra il taglio e la fine della banda

– F4 = Rifinitura tra il taglio e il bordo della merlatura

Il valore di questi tagli è legato alla precisione di lavoro della pressa e alla qualità dello stampo.

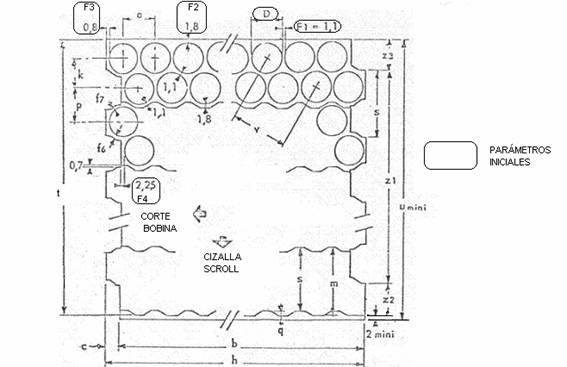
La figura 1 mostra questi parametri iniziali, per una migliore identificazione sono inquadrati in rettangoli.

Facciamo un esempio per seguire meglio il calcolo,

Supponiamo i seguenti valori per un certo tappo:

D = 92 mm.

N1 =18 ( 2 file di 9)

N2 = 5

F1 = 1,1 mm tra fette contigue

F2 = 1,8 mm tra il taglio e il bordo laterale del nastro

F3 = 0,8 mm tra il taglio e la fine della banda

F4 = 2,25 mm tra il taglio e il bordo della merlatura

Vedere la figura nº 1 qui sotto. In esso abbiamo rappresentato con lettere le diverse dimensioni che definiscono i diversi parametri dello schema di taglio.

Abbiamo anche segnato con due frecce le direzioni di avanzamento del materiale nelle operazioni di taglio a bobina e taglio a cesoia. Ora svilupperemo il calcolo delle diverse dimensioni.

1º.- Distanza tra due tagli: a = D + F1 ( a = 92 + 1.1 = 93.1 )

Questo valore a corrisponde alla velocità di avanzamento nella pressa.

2º.- Lunghezza di taglio della bobina: b = a x (N1/2 – 1) + D + 2F1

( b = 93,1 x 18/2 – 1) + 92 + 2 x 0,8 = 838,4 )

È il passo di alimentazione sulla linea di taglio delle bobine.

3º.- Profondità della merlatura nel rotolo primario: c = a/2 – F3 + F4

( c = 93.1/2 – 0.8 + 2.25 = 48 )

4º.- Lunghezza delle foglie: h = b + c ( h = 838.4 + 48 = 886.4 )

5º.- Distanza tra le file centrali dello stesso cuscino:

k = a/2 x 1/ tg30º k = a/2 x 1/ tg30º k = a/2 x 1/ tg30º

k = 93,1 /2 x 1/ 0,57733 = 80,624

6º.- Larghezza di banda: m = 2F2 + D + k ( m = 2 x 1.8 + 92 + 80.624 =176.224 )

7º.-Distanza tra le linee centrali di due file contigue di due cuscini:

p = V (2F1 + D)(2F1 + D) – (F1/2 + D/2) (F1/2 + D/2)

p = V (2 x 1,1 + 92 ) (2 x 1,1 + 92 ) – (1,1/2 + 92/2) (1,1/2 + 92/2) = 81,894

8º.- Altezza della merlatura in pergamena secondaria: q = D + 2F2 – p

( q = 92 + 2 x 1,8 – 81,894 = 13,706 )

9º.- Passo di taglio in cesoia: s = m – q ( s = 176.224 -13.706 = 162.518 )

10º.- Larghezza netta del foglio (senza rifilatura): t = ( N2 – 1 ) s + m

t = (5 -1 ) x 162,518 + 176,224 = 826,296

11º.- Larghezza minima del foglio (larghezza della bobina) : u = t + rifilatura minima

( u = 826.296 + 2 = 828.296 )

Questa cifra è arrotondata per eccesso, quindi 829 mm sarebbe la larghezza della bobina richiesta.

12º.- Distanza tra i centri dei punzoni nelle matrici a cappuccio.

v = V ( a ( a + D/2 +F1/2) x ( a + D/2 +F1/2) + k x k

v = V ( 93.1 + 92/2 + 1.1/2 ) x ( 93.1 + 92/2 + 1.1/2 ) + 80.624 x 80.624 = 161.252

13º.- Distanza tra i merli estremi: z1 = t – m

( z1 = 826.296 -176.224 = 650.072)

14º.- z2 = k ( z2 = 80.624 )

15º.- z3 = t -z1 -z2 ( z3 = 826.296 – 650.072 – 80.624 = 95.6 )

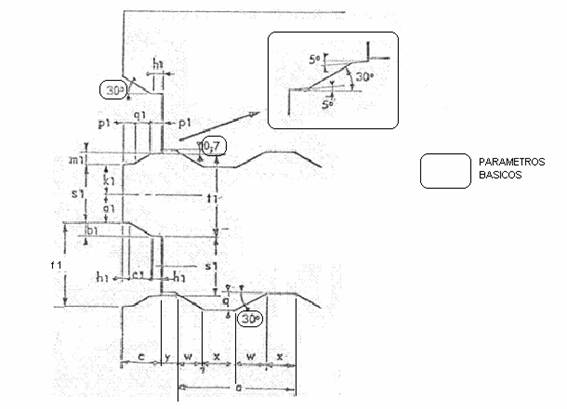
Finora le misure principali del foglio. Entriamo ora nella definizione delle misure dettagliate dei profili della merlatura primaria e secondaria. Per fare questo seguiremo le dimensioni definite nella figura nº 2.

Parametri di base:

A) L’angolo del pendio sui merli, sia il rotolo primario che quello secondario, è di 30º.

B) Lo spostamento dell’inizio di taglio del rotolo secondario, rispetto all’apice della crenatura del rotolo primario, è di 0,7 mm. Questo assicura che il taglio sarà pulito, senza produrre spine sui bordi.

C) Per facilitare lo stesso effetto di cui sopra, la pendenza della cresta della coclea primaria, coincidente con il taglio della coclea secondaria, ha una pendenza composta, con due inclinazioni 5º e 30º. Vedi dettaglio nella figura nº 2

Figura 2

16º.- Lunghezza di pendenza del coronamento secondario: w = q /tg 30º.

(w = 13.706 /0.57733 = 23.74 )

17º. Lunghezza della base del coronamento secondario: x = ( a – 2w )/2

(x = (93,1 – 2 x 23,74)/2 = 22,81)

18º.- a1 = k – D/2 – F2 ( a1 = 80.624 – 92/2 – 1.8 = 32.824 )

19º.- b1 = k – 2 a1 ( b1 = 80.624 – 2 x 32.824 = 14.976 )

20º.- c1 = b1/ tg30º ( c1 = 14.976/0.5773 = 25.94 )

21º.- h1 = ( c – c1 )/2 h1 = ( 48 – 25,94 )/2 = 11,03

22º.- k1 = p – D/2 – F2 + 0,7 ( k1 = 81,894 – 46 – 1,8 + 0,7 = 34,794 )

23º.- m1 = p – 2k1 ( m1 = 81,894 – 2 x 34,794 = 12,306 )

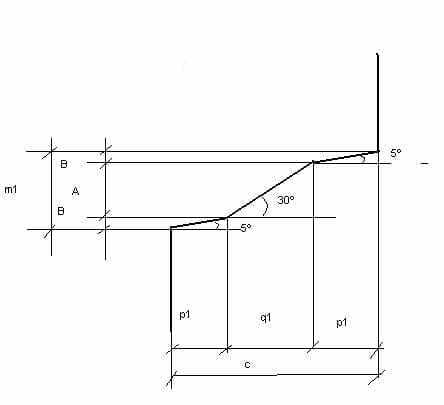
24º e 25º.- Per calcolare le coordinate p1 e q1 guarderemo la figura nº 3.

In esso si compie la seguente equazione:

c = 2p1 + q1

m1 = 2B + A, B = p1 x tg 5º, A = q1 x tg 30º.

Quindi m1 = 2p1 x tg5º + q1 x tg30º = 0,176 p1 + 0,5773 q1

Perciò l’equazione con due incognite è dichiarata come segue:

c = 2p1 + q1

m1 = 0,176p1 + 0,5773 q1

ma poiché c e m1 sono valori già noti, avremmo:

2p1 + q1 = 48

0,176p1 + 0,5773 q1 = 12,306

se risolviamo questa espressione otteniamo i seguenti valori:

p1 = 15,741 ql = 16,518

26º.- Calcolo della y :

Nella figura nº 2 si compie che:

c + y + w – p1 = w + x + w, semplificando:

c + y – p1 = w + x, da cui:

y = w + x + p1 – c

y = 23.74 + 22.81 + 15.741 – 48 = 14.291

27º.- s1 = k1 + a1 ( s1 = 34.794 + 32.824 = 67.618 )

28º.- f1 = m1 + s1 + b1 ( f1 = 12.306 + 67.618 + 14.976 = 94.9 )

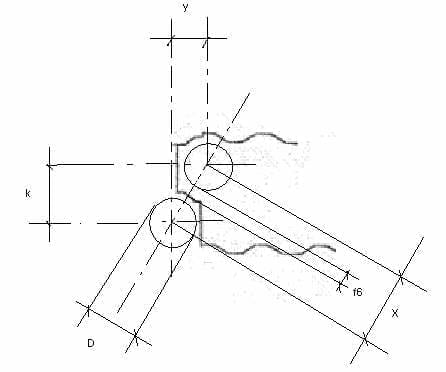
29º.- f6 Per calcolare questo taglio, useremo la figura nº 4. In esso si compie:

1°) y = D/2 + F3 + F4 – F/2

y = 92/2 + 0.8 + 2.25 – 1.1/2 = 48.5

2º) x = V k*k + y*y

x = V 80.624×80.624 + 48.5×48.5 = 94.087

3º) f6 = ( x – D )/ 2

f6 = (94.087 – 92 ) / 2 = 1.0435

Figura 4

30º.- f7. Con un ragionamento analogo al precedente avremmo:

1º) x’ = V p*p + y*y

x’ = V 81,894×81,894+ 48,5×48,5 = 95,178

3º) f7 = ( x’ – D )/ 2

f6 = (95.178– 92 ) / 2 = 1.589

È possibile preparare o ottenere un piccolo programma per computer per il calcolo di tutti questi valori, senza bisogno di operare a mano.

Torna al processo di Can World