Nous allons définir de manière très simple chacun des concepts de base utilisés dans un système de contrôle de la qualité par des variables appliquées dans l’inspection des conteneurs.

Nous allons d’abord définir ce que nous entendons par variables.

QUELS TYPES DE VARIABLES CONNAISSONS-NOUS ?
Il existe deux types de variables à prendre en compte, les variables continues et les variables discrètes.

Variables continues
Les variables continues sont celles qui sont mesurées.
Variables discrètes
Les variables discrètes sont comptées.
Les premiers donnent lieu à un contrôle par variables et les seconds à un contrôle par attributs.

Les caractéristiques de qualité que nous appellerons variables sont toutes celles qui peuvent être représentées par un nombre. Par exemple, la taille d’un boulon, la résistance des résistances des fils, la teneur en cendres du carbone, etc.
Les attributs sont les caractéristiques de qualité non mesurables, dont la taille ne peut généralement pas être représentée par un nombre. Comme par exemple nous pouvons prendre les imperfections visuelles des surfaces des produits, telles que les taches, les différences de ton, les aspects d’une soudure, etc, etc, etc.
Enfin, nous devons tenir compte du fait que tant les processus que les lots finis peuvent être contrôlés par des attributs ou par des variables.

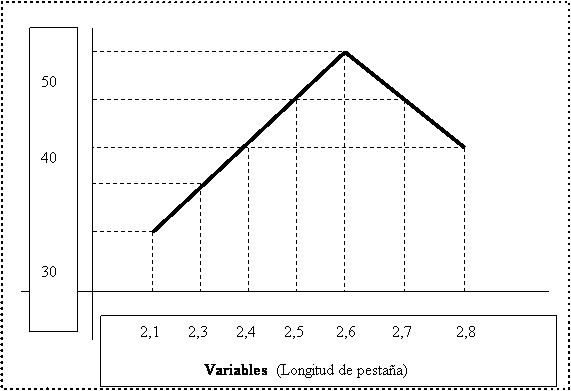
Le meilleur moyen est d’utiliser un exemple pratique. Supposons que nous contrôlions la longueur de la bride du corps du conteneur. Après une série de mesures, nous en faisons un graphique comme le montre la figure nº 1. Nous prenons sur l’axe des abscisses les valeurs trouvées pour les longueurs des brides et sur l’ordonnée le nombre de conteneurs.

Avec ce graphique en vue, nous allons définir comment :

Variable: Le paramètre à mesurer. Dans ce cas, la longueur du cil.

Fréquence: Nombre de fois qu’une variable est répétée. Dans notre exemple, le nombre de conteneurs.

Trajectoire : la plage sur laquelle une variable se déplace. Entre 2,1 et 2,8 mm (valeurs de longueur de la bride)

Intervalle: regroupement des valeurs d’une variable dans une certaine plage. Par exemple : regroupement de toutes les valeurs comprises entre 2,3 et 2,4 en valeur 2,4.

Amplitude: Différence entre les valeurs extrêmes de la trajectoire. Dans notre exemple de tabulations : 2,8 – 2,1 = 0,7 d’amplitude.

Moyenne: (ou moyenne arithmétique) : somme de toutes les valeurs divisée par le nombre total de données.

X = (10*2.1 + 20*2.3 + 30*2.4 + 40*2.5 + 50*2.6 + 40*2.7 + 30*2.8) / (10 + 20 + 30 + 40 + 50 + 40 + 30 ) = ( 21 + 46 + 72 + 100 + 130 + 108 + 84) / 220 = 2.55

Médiane : la valeur de la distribution, supposée être ordonnée du plus petit au plus grand, qui a le même nombre de fréquences à sa gauche et à sa droite, c’est-à-dire la valeur qui occupe la place centrale, en supposant un nombre impair de données. Si le nombre de données est pair, on peut dire qu’il y a deux valeurs médianes et que la moyenne arithmétique est prise entre elles.

Poursuivant l’exemple précédent de la longueur des cils, nous aurions

Fréquences = 10 + 20 + 30 + 40 + 50 + 40 + 40 + 30 = 220

220 serait la fréquence absolue ou cumulative

Fréquence centrale = 220 / 2 = 110

Par conséquent, la médiane serait :
2.6
puisque c’est la valeur de la variable qui occupe la 110e place à partir du début.

Fréquence Fréquence cumulée Variable (m/m)

10 10 2,1

20 30 2,3

30 60 2,4

40 100 2,5

50 150 2,6

40 190 2,7

30 220 2,8

Plus d’informations dans :

http://html.rincondelvago.com/control-de-calidad-estadistico.html

Retour à Contrôle mondial de Can