我们将通过一种非常简单的方式来定义质量控制系统中使用的每个基本概念，方法是通过检查容器中使用的变量。

在定义变量的含义之前。

我们知道什么类型的变量？
有两种类型的变量需要考虑，连续变量和离散变量。

连续变量
连续变量是要测量的变量。
离散变量
计算离散变量。
第一个产生变量控制，第二个产生属性控制。

我们称之为变量的质量特征就是所有可以用数字表示的特征。 例如，螺栓的测量，线电阻的电阻，煤中灰分的含量等。
这些属性是那些不可测量的质量特征，其尺寸通常不能用数字表示。 例如，我们可以采取产品表面的视觉缺陷，例如污点，色调差异，焊缝方面等。
最后，我们必须记住，可以通过属性或变量来检查过程和成品批次。

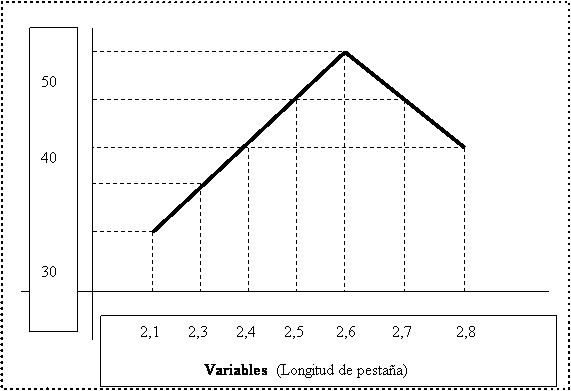
最好的方法是使用实际示例。 假设我们正在控制容器主体的法兰长度。 经过一系列的测量，我们用它们制作了一张图，如图1所示。 我们携带在横坐标轴上找到的法兰长度值和纵坐标中的容器数找到的值。

鉴于此图，我们将定义为：

多变的：要测量的参数。 在这种情况下，法兰长度。

频率：重复变量的次数。 在我们的示例中，包数。

路线：变量移动的范围。 在2.1到2.8毫米之间（法兰长度值）

间隔：在特定路径内对变量的值进行分组。 例如：将值2.3和2.4之间的所有值分组为值2.4。

振幅：路线的极端值之间的差异。 在我们的标签示例中：2.8-2.1 = 0.7宽度。

平均值：（或算术平均值）：所有值的总和除以数据总数

X =（10 * 2.1 + 20 * 2.3 + 30 * 2.4 + 40 * 2.5 + 50 * 2.6 + 40 * 2.7 + 30 * 2.8）/（10 + 20 + 30 + 40 + 50 + 40 + 30）=（21 + 46 + 72 + 100 + 130 + 108 + 84）/ 220 = 2.55

中位数：假设分布的值是从最小到最大排序的，则该值在左边和右边留下相同数量的频率，也就是说，假设数据数量为奇数，则该值占据中心位置。 如果数据的数量是偶数，可以说有两个中值并且取它们之间的算术平均值。

继续前面的法兰长度示例，我们将得到：

频率= 10 + 20 + 30 + 40 + 50 + 40 + 30 = 220

220将是绝对或累积频率

频率中心= 220/2 = 110

因此，中位数将： 2.6 ，因为这是从一开始就占据第110位的变量的值。

频率可变累计频率（m / m ）

10 10 2,1

20 30 2,3

30 60 2,4

40 100 2,5

50 150 2,6

40 190 2,7

30 220 2,8

更多信息，请参见：

http://html.rincondelvago.com/control-de-calidad-estadistico.html

回到控制世界罐头