Мы будем очень просто определять каждую из основных концепций, используемых в системе контроля качества, с помощью переменных, применяемых при проверке контейнеров.

Сначала мы определим, что мы имеем в виду под переменными.

КАКИЕ ТИПЫ ПЕРЕМЕННЫХ МЫ ЗНАЕМ?
Существует два типа переменных, которые следует учитывать — Непрерывные переменные и Дискретные переменные.

Непрерывные переменные
Непрерывные переменные — это те, которые измеряются.
Дискретные переменные
дискретные переменные подсчитываются.
Первые вызывают управление по переменным, а вторые — по атрибутам.

Качественные характеристики, которые мы будем называть переменными, это все те, которые могут быть представлены числом. Например, размер болта, сопротивление проволочных резисторов, содержание золы в углероде и т.д., и т.п. и т.п.
Атрибутами являются те не поддающиеся измерению качественные характеристики, размер которых, как правило, не может быть представлен числом. В качестве примера можно взять визуальные несовершенства поверхностей изделий, такие как пятна, различия в тоне, аспекты сварного шва и т.д. и т.п. и т.п.
Наконец, мы должны учитывать, что как процессы, так и готовые партии могут быть проверены по атрибутам или по переменным.

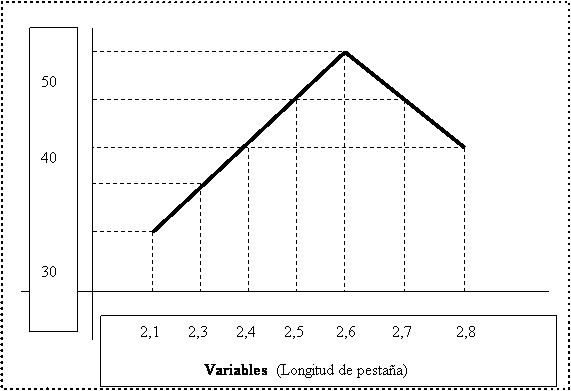
Лучший способ — использовать практический пример. Предположим, мы контролируем длину фланца корпуса контейнера. После серии измерений мы делаем график с ними, как показано на рисунке nº 1. Мы берем по оси абсцисса значения, найденные для длины фланцев, а по ординате — количество контейнеров.

С помощью этого графика мы определим, как это сделать:

Переменная: Измеряемый параметр. В данном случае длина ресницы.

Частота: Количество повторений переменной. В нашем примере количество контейнеров.

Путь: Диапазон, по которому перемещается переменная. Между 2,1 и 2,8 мм (Значения длины фланца)

Интервал: группировка значений переменной в определенном диапазоне. Например: Группировка всех значений между 2.3 и 2.4 в значение 2.4.

Амплитуда: Разница между экстремальными значениями пути. В нашем примере вкладок: 2.8 — 2.1 = 0.7 амплитуды.

Среднее: (или среднее арифметическое): Сумма всех значений, деленная на общее количество данных.

X = (10*2.1 + 20*2.3 + 30*2.4 + 40*2.5 + 50*2.6 + 40*2.7 + 30*2.8) / (10 + 20 + 30 + 40 + 50 + 40 + 30 ) = ( 21 + 46 + 72 + 100 + 130 + 108 + 84) / 220 = 2.55

Медиана: Значение распределения, которое предполагается упорядочить от наименьшего к наибольшему, которое имеет одинаковое количество частот слева и справа, то есть значение, которое занимает центральное место, предполагая нечетное количество данных. Если число данных четное, то можно сказать, что есть два средних значения и среднее арифметическое берется между ними.

Продолжая предыдущий пример с длиной ресниц:

Частоты = 10 + 20 + 30 + 40 + 50 + 40 + 40 + 30 = 220

220 будет абсолютной или совокупной частотой

Центральная частота = 220 / 2 = 110

Следовательно, медиана была бы:
2.6
так как это значение переменной, которая занимает 110-е место, начиная с начала.

Частота Суммарная частота Переменная (м/м)

10 10 2,1

20 30 2,3

30 60 2,4

40 100 2,5

50 150 2,6

40 190 2,7

30 220 2,8

Больше информации:

http://html.rincondelvago.com/control-de-calidad-estadistico.html

Назад в Can World Control