INTRODUCTION
Dans la seconde moitié du siècle dernier, la nécessité de réduire les coûts a progressivement mis en œuvre l’impératif de tirer le meilleur parti de la surface métallique dédiée à la fabrication des bouchons et fonds. À cette fin, la découpe en zig-zag a d’abord été introduite dans les bandes de presse, puis la même technique a été utilisée pour découper des feuilles à partir de bobines.
L’objectif de cet article est de présenter les notions de base pour le calcul de la silhouette, ou du profil, de ces coupes en zigzag. En espagnol, pour désigner ce type de tonte, l’utilisation du mot anglais « scroll shearing » s’est généralisée. C’est pourquoi nous utiliserons dorénavant ce terme. Nous appellerons coupe en spirale primaire celle effectuée sur les lignes de coupe de bobines, et coupe en spirale secondaire celle effectuée sur les cisailles pour la préparation de bandes ou de courroies pour les presses.
Bien que les bandes soient parfois utilisées pour des matrices simples – poinçon simple – et ne contiennent donc qu’une seule rangée de fonds, le cas le plus courant est celui des matrices doubles, c’est-à-dire des bandes à double rangée. La présente étude se concentrera donc sur ce dernier type.
RÉGLAGES INITIAUX
Pour commencer le calcul, nous avons besoin de connaître certaines données au préalable. C’est le cas :
– D = Le diamètre de coupe du matériau nécessaire pour découper le couvercle. Elle doit avoir été préalablement calculée et vérifiée sur le plan pratique.
– N1 = Nombre de coupes à obtenir par bande. Nous serons limités par :
– le pas de coupe maximum/minimum de la ligne de refendage des bobines.
– la largeur de feuille maximale/minimale autorisée par la cisaille à spirale.
– la longueur de bande maximale/minimale que la presse acceptera.
Ces données seront indiquées dans les manuels des machines.
– N2 = Nombre de bandes que nous voulons obtenir par feuille. Il sera limité par :
– la largeur maximale/minute de la bobine que la ligne de refendage peut traiter.
– la longueur maximale/minimale de la feuille que la cisaille à rouleau peut traiter.
– F1 = Découpage minimum entre les coupes.
– F2 = Découpe entre la coupe et le bord latéral de la bande
– F3 = Découpe entre la coupe et le bout de la bande
– F4 = Bordure entre la coupe et le bord du créneau
La valeur de ces découpes est liée à la précision du travail de la presse et à la qualité de la matrice.
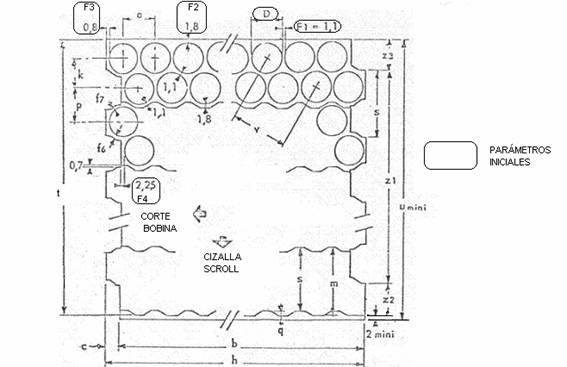
La figure 1 montre ces paramètres initiaux, pour une meilleure identification, ils sont encadrés par des rectangles.
Donnons un exemple pour mieux suivre le calcul,
Supposons les valeurs suivantes pour un certain plafond :
D = 92 mm.
N1 =18 ( 2 rangées de 9)
N2 = 5
F1 = 1,1 mm entre les tranches contiguës
F2 = 1,8 mm entre la coupe et le bord latéral de la bande
F3 = 0,8 mm entre la coupe et l’extrémité de la bande
F4 = 2,25 mm entre la coupe et le bord de crénelage
Voir la figure n° 1 ci-dessous. Nous y avons représenté par des lettres les différentes dimensions qui définissent les différents paramètres du schéma de coupe.
Nous avons également marqué avec deux flèches, les directions d’alimentation en matière dans les opérations de coupe de bobines et de cisailles à spirales. Nous allons maintenant développer le calcul des différentes dimensions.
1º.- Distance entre deux coupes : a = D + F1 ( a = 92 + 1,1 = 93,1 )
Cette valeur a correspond à la vitesse d’avance dans la presse.
2º.- Longueur de coupe de la bobine : b = a x (N1/2 – 1) + D + 2F1
( b = 93,1 x 18/2 – 1) + 92 + 2 x 0,8 = 838,4 )
Il s’agit de l’étape d’alimentation de la ligne de refendage des bobines.
3º – Profondeur de crénelage dans le parchemin primaire : c = a/2 – F3 + F4
( c = 93.1/2 – 0.8 + 2.25 = 48 )
4º.- Longueur de la feuille : h = b + c ( h = 838,4 + 48 = 886,4 )
5º.- Distance entre les rangées centrales d’un même coussin :
k = a/2 x 1/ tg30º k = a/2 x 1/ tg30º k = a/2 x 1/ tg30º
k = 93,1 /2 x 1/ 0,57733 = 80,624
6º.- Largeur de bande : m = 2F2 + D + k ( m = 2 x 1,8 + 92 + 80,624 =176,224 )
7º.-Distance entre les lignes centrales de deux rangées contiguës de deux coussins :
p = V (2F1 + D)(2F1 + D) – (F1/2 + D/2) (F1/2 + D/2)
p = V (2 x 1,1 + 92 ) (2 x 1,1 + 92 ) – (1,1/2 + 92/2) (1,1/2 + 92/2) = 81,894
8º – Hauteur du rempart dans le rouleau secondaire : q = D + 2F2 – p
( q = 92 + 2 x 1,8 – 81,894 = 13,706 )
9º.- Pas de cisaillement dans la cisaille de défilement: s = m – q ( s = 176,224 -13,706 = 162,518 )
10º – Largeur nette de la feuille (sans rognage) : t = ( N2 – 1 ) s + m
t = (5 -1 ) x 162,518 + 176,224 = 826,296
11º.- Largeur minimale de la feuille (largeur de la bobine) : u = t + ro gnage minimal
( u = 826.296 + 2 = 828.296 )
Ce chiffre est arrondi à la hausse, de sorte que 829 mm serait la largeur de bobine requise.
12º.- Distance entre les centres des poinçons dans les matrices des bouchons.
v = V ( a ( a + D/2 +F1/2) x ( a + D/2 +F1/2) + k x k
v = V ( 93,1 + 92/2 + 1,1/2 ) x ( 93,1 + 92/2 + 1,1/2 ) + 80,624 x 80,624 = 161,252
13º.- Distance entre les créneaux extrêmes : z1 = t – m
( z1 = 826.296 -176.224 = 650.072)
14º.- z2 = k ( z2 = 80,624 )
15º.- z3 = t -z1 -z2 ( z3 = 826,296 – 650,072 – 80,624 = 95,6 )
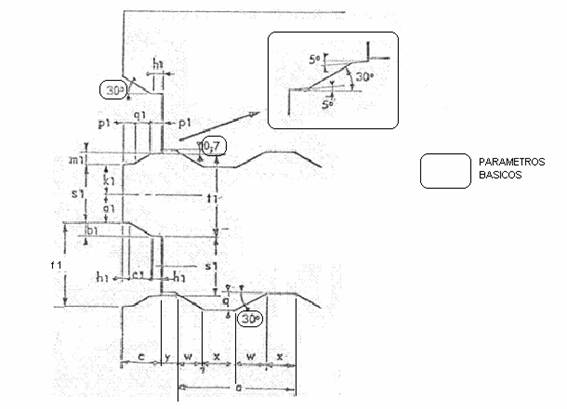
Jusqu’à présent, les principales mesures de la feuille. Nous entrons maintenant dans la définition des mesures détaillées des profils de crénelage des parchemins primaires et secondaires. Pour ce faire, nous suivrons les dimensions définies dans la figure nº 2.
Paramètres de base :
A) L’angle de la pente sur les créneaux, tant sur le rouleau primaire que sur le rouleau secondaire, est de 30º.
B) Le déplacement du début de la coupe du rouleau secondaire, par rapport au sommet du créneau du rouleau primaire, est de 0,7 mm. Cela garantit que la coupe sera propre et ne produira pas d’épines sur les bords.
C) Pour faciliter le même effet que ci-dessus, la pente de la crête du rouleau primaire, qui coïncide avec la coupure du rouleau secondaire, a une pente composée, avec deux inclinaisons de 5º et 30º. Voir détail dans la figure nº 2
Figure 2
16º.- Longueur de la pente du rempart secondaire : w = q /tg 30º.
(w = 13.706 /0.57733 = 23.74 )
17º. Longueur de la base du rempart du rouleau secondaire : x = ( a – 2w )/2
(x = (93,1 – 2 x 23,74)/2 = 22,81)
18º.- a1 = k – D/2 – F2 ( a1 = 80,624 – 92/2 – 1,8 = 32,824 )
19º.- b1 = k – 2 a1 ( b1 = 80,624 – 2 x 32,824 = 14,976 )
20º.- c1 = b1/ tg30º ( c1 = 14,976/0,5773 = 25,94 )
21º.- h1 = ( c – c1 )/2 h1 = ( 48 – 25,94 )/2 = 11,03
22º.- k1 = p – D/2 – F2 + 0,7 ( k1 = 81,894 – 46 – 1,8 + 0,7 = 34,794 )
23º.- m1 = p – 2k1 ( m1 = 81,894 – 2 x 34,794 = 12,306 )
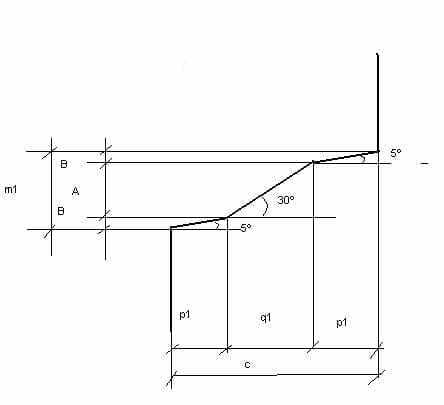
24º et 25º – Pour calculer les coordonnées p1 et q1, nous allons regarder la figure n° 3.
L’équation suivante y est remplie :
c = 2p1 + q1
m1 = 2B + A, B = p1 x tg 5º , A = q1 x tg 30º.
Donc m1 = 2p1 x tg5º + q1 x tg30º = 0,176 p1 + 0,5773 q1
Par conséquent, l’équation avec deux inconnues est énoncée comme suit :
c = 2p1 + q1
m1 = 0,176p1 + 0,5773 q1
mais puisque c et m1 sont des valeurs déjà connues, nous l’aurions fait :
2p1 + q1 = 48
0,176p1 + 0,5773 t1 = 12,306
si nous résolvons cette expression, nous obtenons les valeurs suivantes :
p1 = 15,741 ql = 16,518
26º.- Calcul de l’y :
Dans la figure n° 2, il est répondu à cette question :
c + y + w – p1 = w + x + w, en simplifiant :
c + y – p1 = w + x, d’où :
y = w + x + p1 – c
y = 23.74 + 22.81 + 15.741 – 48 = 14.291
27º.- s1 = k1 + a1 ( s1 = 34,794 + 32,824 = 67,618 )
28º.- f1 = m1 + s1 + b1 ( f1 = 12,306 + 67,618 + 14,976 = 94,9 )
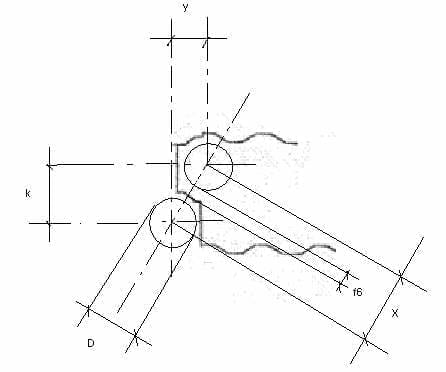
29º.- f6 Pour calculer cette coupe, nous utiliserons la figure n° 4. Elle s’y réalise :
1er) y = D/2 + F3 + F4 – F/2
y = 92/2 + 0.8 + 2.25 – 1.1/2 = 48.5
2º) x = V k*k + y*y
x = V 80,624×80,624 + 48,5×48,5 = 94,087
3º) f6 = ( x – D )/ 2
f6 = (94.087 – 92 ) / 2 = 1.0435
Figure 4
30º.- f7. Par un raisonnement analogue au précédent, nous l’aurions fait :
1º) x’ = V p*p + y*y
x’ = V 81,894×81,894+ 48,5×48,5 = 95,178
3º) f7 = ( x’ – D )/ 2
f6 = (95.178– 92 ) / 2 = 1.589
Il est possible de préparer ou de se procurer un petit programme informatique pour le calcul de toutes ces valeurs, sans avoir besoin d’opérer à la main.













0 commentaires