L’objectif est de calculer aussi approximativement que possible, quel est le volume vide de l’intérieur d’une double fermeture de récipients cylindriques afin de pouvoir estimer le volume maximum de caoutchouc que nous devons mettre dans un couvercle, sans endommager la formation de la fermeture, et peut maintenir l’étanchéité du récipient.
Nous utiliserons les dimensions des fixations indiquées dans la recommandation SEFEL Nº1 (1999) et, à l’intérieur de celles-ci, une valeur de serrage nominale et une valeur de serrage à la limite supérieure (très serrée), qui nous permettront de définir la tolérance de travail pour le processus de caoutchoutage.
Toutes les mesures seront représentées en millimètres, le volume sera donc établi en mm3.
Le modèle mathématique qui est établi est approximatif, car il ne s’agira pas toujours d’une ellipse parfaite, en fonction des caractéristiques du métal et des profils des rouleaux utilisés.
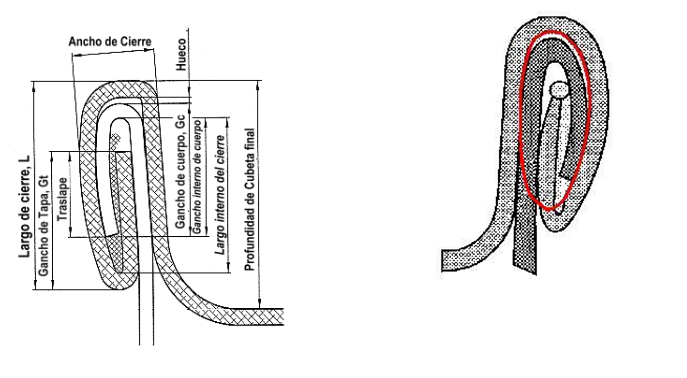
SURFACE DE LA SECTION D'ÉTANCHÉITÉ
Pour des raisons pratiques, nous considérons la section de fermeture comme une ellipse. Pour un calcul plus précis, nous ne considérons que l’ellipse de l’intérieur, de sorte que le matériau extérieur laissé par le couvercle n’intervient pas. Cela pourrait être représenté comme suit :
Dans cette ellipse intérieure, nous devons calculer la surface de toute la section marquée :
Où L=Longueur de l’ellipse, et est égale à la longueur de la fermeture moins deux fois l’épaisseur du couvercle, et E la largeur de l’ellipse, égale à la largeur de la fermeture, également moins deux fois l’épaisseur du couvercle.
Selon cette formule, la formule ci-dessus serait la suivante :
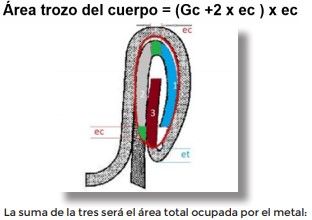
Nous calculons ensuite la surface occupée par le métal à l’intérieur de l’ellipse. Cette zone est composée de trois segments : deux correspondant au corps et un au couvercle.
Les deux crochets (corps et couvercle) et un troisième segment formé par le corps et la courbe supérieure de celui-ci.
Nous déterminons la surface de chacun d’entre eux :
1 Le crochet du corps, légèrement courbé, considérons-le comme sa longueur, et un facteur de correction de 10% pour la courbure. Votre domaine serait :
2 Le crochet du couvercle ne rentre pas en entier, mais la partie qui reste à l’extérieur correspond à une longueur égale à l’épaisseur du matériau. Par conséquent, votre zone serait :
3 La pièce du corps qui entre à l’intérieur de l’ellipse interne de l’attache est considérée comme une longueur égale à Gc mais elle a aussi une correction, correspondant à la courbe et à l’excès de sa longueur, qui entre à l’intérieur de l’ellipse ; nous pouvons donc considérer qu’elle correspond à sa longueur plus deux épaisseurs de métal, une pour l’excès et une pour la courbe du crochet : Ainsi :
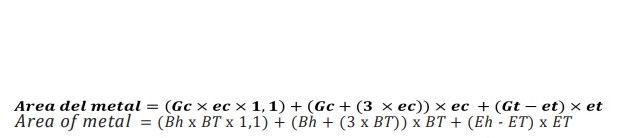
Équation 3
Par conséquent, la surface libre de la section de l’ellipse ci-dessus est égale à la soustraction des équations 2 et 3. Voyons un exemple pratique, pour un conteneur de diamètre 73 (# 300) avec une fermeture caractéristique dans les dimensions SEFEL I :
Longueur : 2,80 G. Corps : 1,85
Largeur : 1,05 G. Couverture : 1,90
ec = 0,16 Chevauchement : 1,1
et = 0,20 %Compacité 87%.
Pour une fermeture de dimensions données, la surface de l’ellipse interne serait :
Surface = ((2,80 – 0,40) / 2) x ((1,05-0,40) / 2) x π =1,225 mm2 Surface métallique : (1,85×0,16×1,1) + (1,85+0,48) x 0,16 +(1,70x,20) = 1,013 mm2
Surface libre = 1,225 -1,013 = 0,212 mm2
VOLUME DE L’ELLIPSOÏDE INTÉRIEUR DE LA FERMETURE, ET VOLUME LIBRE
Si nous considérons cette surface pour l’épaisseur de 1 mm, nous aurons le volume du cylindroïde de 1 mm de hauteur. En considérant le développement complet de la fermeture, dont nous calculons la longueur comme le diamètre du centre de la section de la fermeture, multiplié par pi, nous aurons un modèle mathématique simple du volume de la fermeture complète. Ainsi, pour un récipient de diamètre nominal 73, la fermeture aura un diamètre moyen de 74 mm. La durée du développement de la fermeture sera donc
Longueur du développement de la serrure =74 x π = 232,48 mm
En continuant avec l’exemple précédent, le volume calculé pour l’intérieur de la fermeture serait :
0,212 x 232,48 = 49,3 mm3 pour occuper 100 % du volume vide.
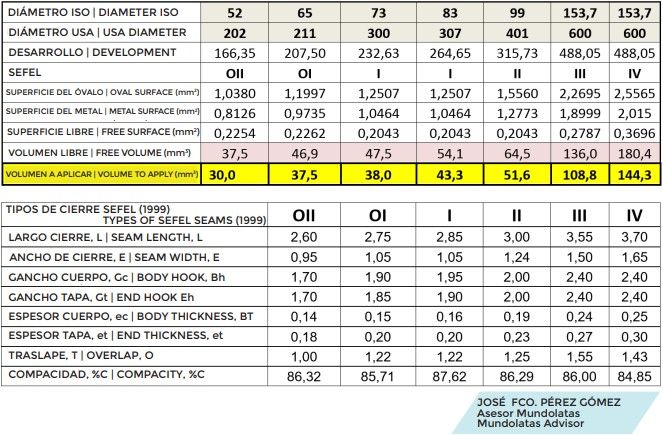
Nous pouvons établir les valeurs d’étanchéité pour les différents diamètres, selon les valeurs SEFEL, avec un degré de serrage selon la norme et pour des valeurs plus serrées, calculant ainsi le volume minimum de caoutchouc nécessaire pour une étanchéité.
VOLUME DES DEMANDES
De manière générale, on peut calculer le volume à occuper par le caoutchouc comme étant 80 % du volume maximal dont nous disposons. Pour calculer les poids, il suffit de multiplier ce volume par la densité du caoutchouc sec, en appliquant la tolérance recommandée par le fournisseur.














0 Comments