Ziel ist es, so annähernd wie möglich zu berechnen, wie groß das Leervolumen des Innenraums eines Doppelverschlusses von zylindrischen Behältern ist, um das maximale Volumen des Gummis abschätzen zu können, das wir in einen Deckel einfüllen sollten, ohne die Formation des Verschlusses zu beschädigen, und das die Dichtheit des Behälters erhalten kann.
Wir werden die in der SEFEL-Empfehlung Nº1 (1999) angegebenen Schraubenabmessungen und innerhalb dieser einen Nennanzugswert und einen Anzugswert an der oberen Grenze (sehr fest) verwenden, was uns erlaubt, die Arbeitstoleranz für den Gummierungsprozess zu definieren.
Alle Messungen werden in Millimetern dargestellt, so dass das Volumen in mm3 ermittelt wird.
Das mathematische Modell, das erstellt wird, ist ein Näherungswert, da es nicht immer eine perfekte Ellipse sein wird, abhängig von den Eigenschaften des Metalls und den Profilen der verwendeten Rollen.
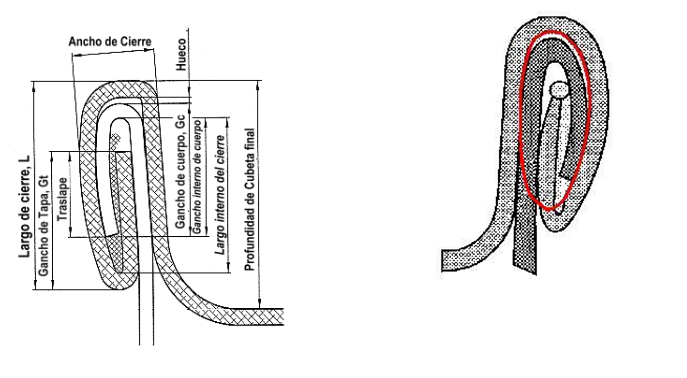
OBERFLÄCHE DES DICHTUNGSPROFILS
Für praktische Zwecke betrachten wir den Verschlussabschnitt als Ellipse. Für eine genauere Berechnung betrachten wir nur die Ellipse des Innenraums, so dass das vom Deckel übrig gebliebene Außenmaterial nicht eingreift. Dies könnte wie folgt dargestellt werden:
In dieser inneren Ellipse müssen wir die Fläche des gesamten markierten Bereichs berechnen:
Wobei L=Länge der Ellipse, und gleich der Länge des Verschlusses minus der doppelten Dicke des Deckels ist, und E die Breite der Ellipse, gleich der Breite des Verschlusses, ebenfalls minus der doppelten Dicke des Deckels.
Demnach würde die obige Formel wie folgt lauten:
Wir berechnen dann die Fläche, die das Metall innerhalb der Ellipse einnimmt. Dieser Bereich setzt sich aus drei Segmenten zusammen: zwei, die dem Körper entsprechen, und eines, das dem Deckel entspricht.
Die beiden Haken (Korpus und Deckel) und ein drittes Segment, das durch den Korpus und die obere Rundung desselben gebildet wird.
Wir bestimmen die Fläche jedes einzelnen von ihnen:
1 Der Körperhaken, leicht gekrümmt, betrachten wir als seine Länge, und einen Korrekturfaktor von 10% für die Krümmung. Ihr Bereich wäre:
2 Der Abdeckhaken passt nicht im Ganzen, sondern der Teil, der außen bleibt, entspricht einer Länge, die der Dicke des Materials entspricht. Ihr Bereich wäre also:
3 Das Stück des Körpers, das in die innere Ellipse des Verbindungselements eintritt, wird als eine Länge gleich Gc betrachtet, aber es hat auch eine Korrektur, die der Kurve und dem Überschuss seiner Länge entspricht, die in die Ellipse eintritt, so dass wir betrachten können, dass sie seiner Länge plus zwei Metalldicken entspricht, eine für den Überschuss und eine für die Hakenkurve: So:
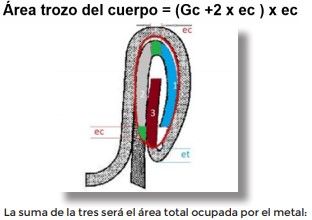
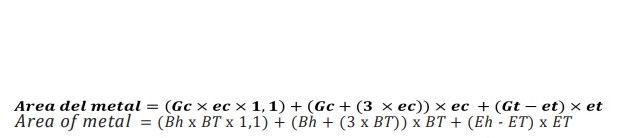
Gleichung 3
Daher ist die freie Fläche des obigen Ellipsenabschnitts gleich der Subtraktion der Gleichungen 2 und 3. Schauen wir uns ein praktisches Beispiel an, für einen Behälter mit Durchmesser 73 (# 300) mit einem charakteristischen Verschluss innerhalb der SEFEL I-Abmessungen:
Länge: 2,80 G. Körper: 1,85
Breite: 1,05 G. Deckel: 1,90
ec = 0,16 Überlappung: 1,1
et = 0,20 %Kompaktheit 87%.
Für einen Abschluss mit gegebenen Abmessungen wäre die Oberfläche der inneren Ellipse:
Fläche = ((2,80 – 0,40) / 2) x ((1,05-0,40) / 2) x π =1,225 mm2 Metalloberfläche: (1,85×0,16×1,1) + (1,85+0,48) x 0,16 +(1,70x,20) = 1,013 mm2
Freie Fläche = 1,225 -1,013 = 0,212 mm2
VOLUMEN DES INNEREN ELLIPSOIDS DES VERSCHLUSSES, UND FREIES VOLUMEN
Wenn wir diese Fläche für die Dicke von 1 mm betrachten, haben wir das Volumen des Zylindroids von 1 mm Höhe. Betrachtet man die komplette Abwicklung des Verschlusses, dessen Länge wir als Durchmesser der Mitte des Verschlussabschnitts, multipliziert mit pi, berechnen, erhält man ein einfaches mathematisches Modell für das Volumen des kompletten Verschlusses. Bei einem Behälter mit dem Nenndurchmesser 73 hat der Verschluss also einen durchschnittlichen Durchmesser von 74 mm. Die Länge der Verschlussentwicklung wird daher
Länge der Schlossabwicklung =74 x π = 232,48 mm
Wenn Sie mit dem vorherigen Beispiel fortfahren, würde das für die Innenseite des Verschlusses berechnete Volumen lauten:
0,212 x 232,48 = 49,3 mm3 , um 100 % des Leervolumens zu belegen.
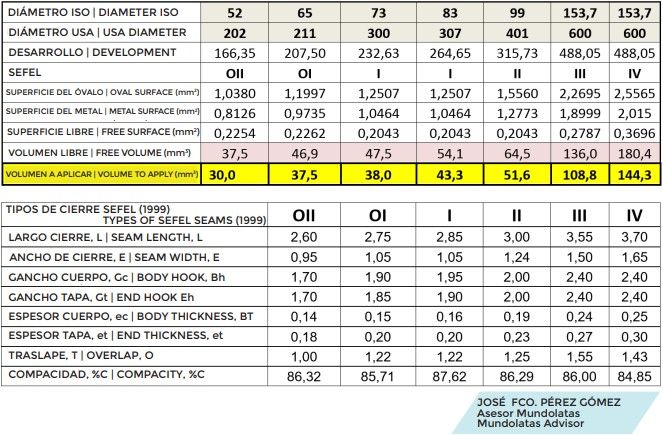
Wir können die Dichtungswerte für die verschiedenen Durchmesser nach SEFEL-Werten, mit einem Anzugsgrad gemäß der Norm und für engere Werte ermitteln und so das für eine Dichtung erforderliche Mindestvolumen an Gummi berechnen.
ANTRAGSVOLUMEN
Als allgemeinen Begriff können wir das vom Gummi zu belegende Volumen mit 80 % des maximalen Volumens berechnen, das wir haben. Um die Gewichte zu berechnen, müssen wir nur dieses Volumen mit der Dichte des trockenen Gummis multiplizieren und dabei die vom Lieferanten empfohlene Toleranz anwenden.















0 Kommentare