O objetivo é calcular, o mais aproximadamente possível, qual é o volume vazio do interior de um duplo fechamento de recipientes cilíndricos, a fim de poder estimar o volume máximo de borracha que devemos colocar em uma tampa, sem danificar a formação do fechamento, e poder manter a estanqueidade do recipiente.
Utilizaremos as dimensões de fixação indicadas na Recomendação SEFEL Nº 1 (1999) e dentro destas, um valor nominal de aperto e um valor de aperto no limite superior (muito apertado), o que nos permitirá definir a tolerância de trabalho para o processo de emborrachamento.
Todas as medidas serão representadas em milímetros, portanto, o volume será estabelecido em mm3.
O modelo matemático que se estabelece é aproximado, pois nem sempre será uma elipse perfeita, dependendo das características do metal e dos perfis dos rolos utilizados.
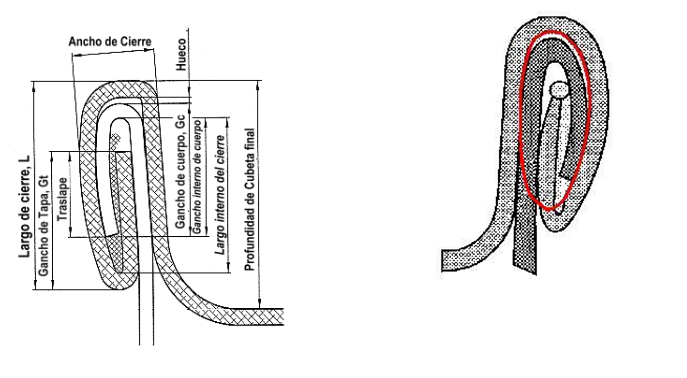
SUPERFÍCIE DA SEÇÃO DE VEDAÇÃO
Para fins práticos, consideramos a seção de fechamento como uma elipse. Para um cálculo mais preciso, consideramos apenas a elipse do interior, para que o material exterior que sobra da tampa não interfira. Isto poderia ser representado da seguinte forma:
Nesta elipse interna, devemos calcular a área de toda a seção marcada:
Onde L=Comprimento da elipse, e é igual ao comprimento do fechamento menos o dobro da espessura da tampa, e E a largura da elipse, igual à largura do fechamento, também menos o dobro da espessura da tampa.
De acordo com isto, a fórmula acima seria a seguinte:
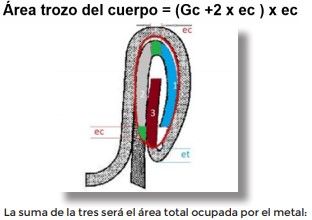
Calculamos então a área ocupada pelo metal dentro da elipse. Esta área é composta de três segmentos: dois correspondentes ao corpo e um à tampa.
Os dois ganchos (corpo e tampa) e um terceiro segmento formado pelo corpo e a curva superior do mesmo.
Nós determinamos a área de cada um deles:
1 O gancho do corpo, ligeiramente curvo, vamos considerá-lo como seu comprimento, e um fator de correção de 10% para a curvatura. Sua área seria:
2 O gancho de cobertura não cabe no todo, mas a parte que permanece fora corresponde a um comprimento igual à espessura do material. Portanto, sua área seria:
3 A peça do corpo que entra dentro da elipse interna do fixador é considerada como um comprimento igual a Gc mas também tem uma correção, correspondente à curva e ao excesso de seu comprimento, que entra dentro da elipse para que possamos considerar que corresponde ao seu comprimento mais duas espessuras de metal, uma para o excesso e outra para a curva do gancho: Assim:
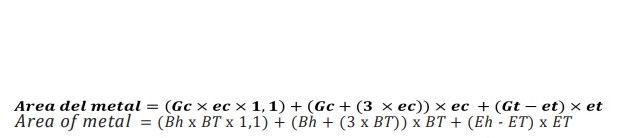
Equação 3
Portanto, a área livre da seção da elipse acima é igual à subtração das equações 2 e 3. Vejamos um exemplo prático, para um recipiente de diâmetro 73 (# 300) com um fechamento característico dentro das dimensões do SEFEL I:
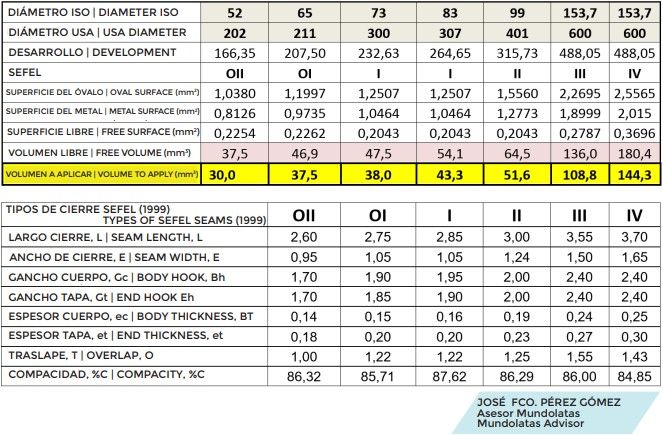
Comprimento: 2,80 G. Corpo: 1,85
Largura: 1,05 G. Cobertura: 1,90
ec = 0,16 Sobreposição: 1,1
et = 0,20 %Compacidez 87%.
Para um fechamento de determinadas dimensões, a superfície da elipse interna seria:
Área = ((2,80 – 0,40) / 2) x ((1,05-0,40) / 2) x π =1.225 mm2 Superfície metálica: (1,85×0,16×1,1) + (1,85+0,48) x 0,16 +(1,70x,20) = 1,013 mm2
Área livre = 1.225 -1.013 = 0.212 mm2
VOLUME DA ELIPSÓIDE INTERNA DO FECHAMENTO, E VOLUME LIVRE
Se considerarmos esta superfície para a espessura de 1 mm, teremos o volume do cilíndroide de 1 mm de altura. Considerando o desenvolvimento completo do fechamento, cujo comprimento calculamos como o diâmetro do centro da seção de fechamento, multiplicado por pi, teremos um modelo matemático simples do volume do fechamento completo. Assim, para um recipiente de diâmetro nominal 73, o fechamento terá um diâmetro médio de 74 mm. A duração do desenvolvimento do fechamento, portanto, será
Comprimento do desenvolvimento da fechadura =74 x π = 232,48 mm
Continuando com o exemplo anterior, o volume calculado para o interior do fechamento seria:
0,212 x 232,48 = 49,3 mm3 para ocupar 100 % do volume vazio.
Podemos estabelecer os valores de vedação para os diferentes diâmetros, de acordo com os valores SEFEL, com um grau de aperto de acordo com o padrão e para valores mais apertados, calculando assim o volume mínimo de borracha necessário para uma vedação.
VOLUME DE APLICAÇÃO
Como um termo geral, podemos calcular o volume a ser ocupado pela borracha como 80% do volume máximo que temos. Para calcular os pesos, basta multiplicar este volume pela densidade da borracha seca, aplicando a tolerância recomendada pelo fornecedor.













0 comentários