INTRODUÇÃO
Na segunda metade do século passado, a necessidade de reduzir os custos tem vindo a implementar gradualmente o imperativo de aproveitar ao máximo a superfície metálica dedicada ao fabrico de tampas e fundos. Para este fim, o corte em zig-zag foi introduzido primeiramente nas teias de prensa e, mais tarde, a mesma técnica foi utilizada para cortar chapas a partir de bobinas.
O objetivo deste trabalho é apresentar as noções básicas para o cálculo da silhueta, ou perfil, desses cortes em zig-zag. Em espanhol, para designar este tipo de tosquia, o uso da palavra inglesa “scroll shearing” (tosquia de pergaminho) tornou-se generalizada. Portanto, vamos usar este termo a partir de agora. Chamaremos de pergaminho primário o corte feito nas linhas de corte da bobina, e pergaminho secundário o corte feito em tesouras para a preparação de tiras ou bandas para prensas.
Embora as tiras sejam por vezes utilizadas para matrizes simples – de punção simples – e portanto contenham apenas uma fila de fundos, o caso mais usual é para matrizes duplas, ou seja, tiras de fila dupla. Este estudo irá, portanto, concentrar-se neste último tipo.
CONFIGURAÇÕES INICIAIS
Para iniciar o cálculo, precisamos de saber alguns dados antes. Estes são:
– D = O diâmetro de corte do material necessário para o corte da tampa. Deve ter sido previamente calculado e praticamente verificado.
– N1 = Número de cortes a serem obtidos por banda. Seremos limitados por:
– o passo máximo/mínimo de corte da linha de corte da bobina.
– a largura máxima/mínima da folha permitida pela tesoura de rolagem.
– o comprimento máximo/mínimo da tira que a prensa aceitará.
Estes dados serão indicados nos manuais das máquinas.
– N2 = Número de bandas que queremos obter por folha. Será limitado por:
– a largura máxima/minuto da bobina que a linha de corte pode suportar.
– o comprimento máximo/mínimo da folha que a tesoura de rolagem pode suportar.
– F1 = Corte mínimo entre cortes.
– F2 = Cortar entre o corte e a borda lateral da banda
– F3 = Aparar entre o corte e a extremidade da banda
– F4 = Aparar entre o corte e a borda do batente
O valor destes cortes está ligado à precisão do trabalho da prensa e à qualidade do molde.
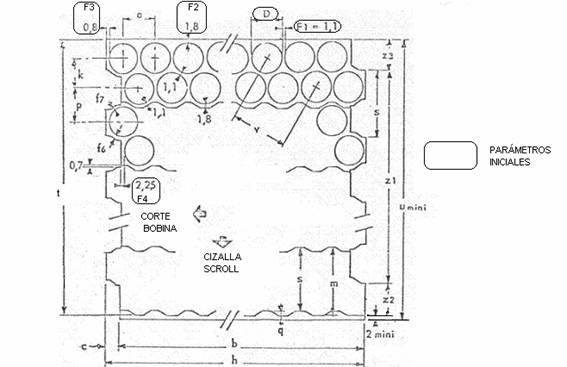
A Figura 1 mostra esses parâmetros iniciais, para melhor identificação eles são enquadrados em retângulos.
Vamos dar um exemplo para seguir melhor o cálculo,
Assumir os seguintes valores para um determinado limite:
D = 92 mm.
N1 =18 ( 2 filas de 9)
N2 = 5
F1 = 1,1 mm entre fatias contíguas
F2 = 1,8 mm entre o corte e a borda lateral da tira
F3 = 0,8 mm entre o corte e a extremidade da fita
F4 = 2,25 mm entre o corte e o bordo de crenelação
Ver figura nº 1 abaixo. Nele temos representado por letras as diferentes dimensões que definem os diferentes parâmetros do esquema de corte.
Também marcamos com duas setas, as direções de alimentação de material nas operações de corte de bobinas e corte de rolo de cisalhamento. Vamos agora desenvolver o cálculo das diferentes dimensões.
1º.- Distância entre dois cortes: a = D + F1 ( a = 92 + 1.1 = 93.1 )
Este valor a corresponde à taxa de alimentação na prensa.
2º – Comprimento de corte da bobina: b = a x (N1/2 – 1) + D + 2F1
( b = 93,1 x 18/2 – 1) + 92 + 2 x 0,8 = 838,4 )
É o passo de alimentação na linha de corte da bobina.
3º – Profundidade da crenelação no rolo primário: c = a/2 – F3 + F4
( c = 93.1/2 – 0.8 + 2.25 = 48 )
4º.- Comprimento das folhas: h = b + c ( h = 838,4 + 48 = 886,4 )
5º – Distância entre as fileiras centrais da mesma almofada:
k = a/2 x 1/ tg30º k = a/2 x 1/ tg30º k = a/2 x 1/ tg30º
k = 93,1 /2 x 1/ 0,57733 = 80,624
6º.- Largura de banda : m = 2F2 + D + k ( m = 2 x 1,8 + 92 + 80,624 =176,224 )
7º -Distância entre linhas centrais de duas filas contíguas de duas almofadas:
p = V (2F1 + D)(2F1 + D) – (F1/2 + D/2) (F1/2 + D/2)
p = V (2 x 1.1 + 92 ) (2 x 1.1 + 92 ) – (1.1/2 + 92/2) (1.1/2 + 92/2) = 81.894
8º.- Altura do lote no rolo secundário: q = D + 2F2 – p
( q = 92 + 2 x 1,8 – 81,894 = 13,706 )
9º.- Passo de corte em rolo de corte: s = m – q ( s = 176.224 -13.706 = 162.518 )
10º.- Largura líquida da chapa (sem corte): t = ( N2 – 1 ) s + m
t = (5 -1 ) x 162.518 + 176.224 = 826.296
11º.- Largura mínima da folha (largura da bobina) : u = t + corte mínimo
( u = 826.296 + 2 = 828.296 )
Este número é arredondado para cima, portanto 829 mm seria a largura da bobina necessária.
12º.- Distância entre os centros de punção em matrizes de tampas.
v = V ( a ( a + D/2 +F1/2) x ( a + D/2 +F1/2) + k x k
v = V ( 93,1 + 92/2 + 1,1/2 ) x ( 93,1 + 92/2 + 1,1/2 ) + 80,624 x 80,624 = 161,252
13º.- Distância entre as ameias extremas: z1 = t – m
( z1 = 826.296 -176.224 = 650.072)
14º.- z2 = k ( z2 = 80,624 )
15º.- z3 = t -z1 -z2 ( z3 = 826.296 – 650.072 – 80.624 = 95.6 )
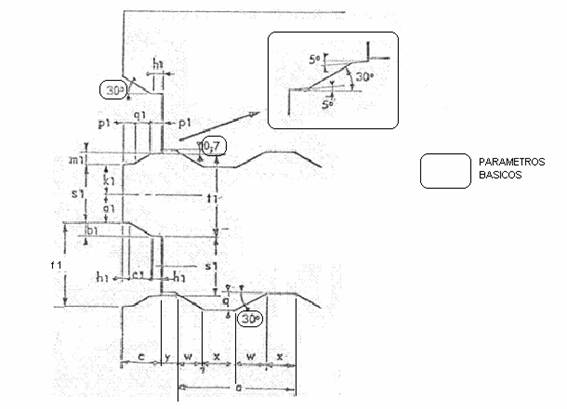
Até agora, as principais medidas da folha. Entramos agora na definição das medidas detalhadas dos perfis de crenelação de rolagem primária e secundária. Para isso, vamos seguir as dimensões definidas na figura nº 2.
Parâmetros básicos:
A) O ângulo da inclinação nas ameias, tanto primária como secundária, é de 30º.
B) O deslocamento do início do corte da rolagem secundária, em relação ao ápice da crenelação da rolagem primária, é de 0,7 mm. Isto garante que o corte será limpo, não produzindo espinhos nas bordas.
C) Para facilitar o mesmo efeito que acima, a inclinação da crista da rolagem primária, coincidindo com o corte da rolagem secundária, tem uma inclinação composta, com duas inclinações de 5º e 30º. Ver detalhe na figura nº 2
Figura 2
16º.- Comprimento da inclinação da colónia de rolamento secundário: w = q /tg 30º.
(w = 13.706 /0.57733 = 23.74 )
17º. Comprimento da base do rolo secundário: x = ( a – 2w )/2
(x = (93,1 – 2 x 23,74)/2 = 22,81)
18º.- a1 = k – D/2 – F2 ( a1 = 80.624 – 92/2 – 1.8 = 32.824 )
19º.- b1 = k – 2 a1 ( b1 = 80.624 – 2 x 32.824 = 14.976 )
20º.- c1 = b1/ tg30º ( c1 = 14.976/0.5773 = 25.94 )
21º.- h1 = ( c – c1 )/2 h1 = ( 48 – 25.94 )/2 = 11.03
22º.- k1 = p – D/2 – F2 + 0,7 ( k1 = 81,894 – 46 – 1,8 + 0,7 = 34,794 )
23º.- m1 = p – 2k1 ( m1 = 81,894 – 2 x 34,794 = 12,306 )
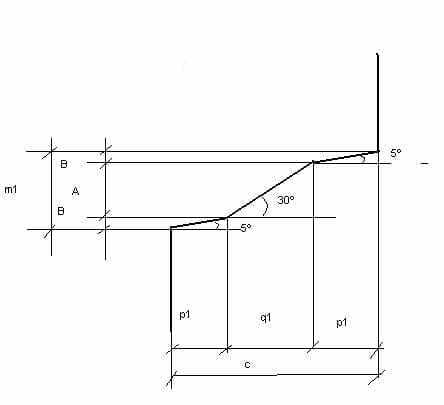
24º e 25º. – Para calcular as coordenadas p1 e q1 veremos a figura nº 3.
Nela se cumpre a seguinte equação:
c = 2p1 + q1
m1 = 2B + A, B = p1 x tg 5º , A = q1 x tg 30º.
Portanto m1 = 2p1 x tg5º + q1 x tg30º = 0,176 p1 + 0,5773 q1
Portanto, a equação com duas incógnitas é apresentada como se segue:
c = 2p1 + q1
m1 = 0,176p1 + 0,5773 q1
mas como C e M1 já são valores conhecidos, nós teríamos:
2p1 + q1 = 48
0,176p1 + 0,5773 q1 = 12,306
se resolvermos esta expressão, obtemos os seguintes valores:
p1 = 15.741 ql = 16.518
26º.- Cálculo do y :
Na figura nº 2 cumpre-se isso:
c + y + w – p1 = w + x + w, simplificando:
c + y – p1 = w + x, de onde:
y = w + x + p1 – c
y = 23.74 + 22.81 + 15.741 – 48 = 14.291
27º.- s1 = k1 + a1 ( s1 = 34.794 + 32.824 = 67.618 )
28º.- f1 = m1 + s1 + b1 ( f1 = 12,306 + 67,618 + 14,976 = 94,9 )
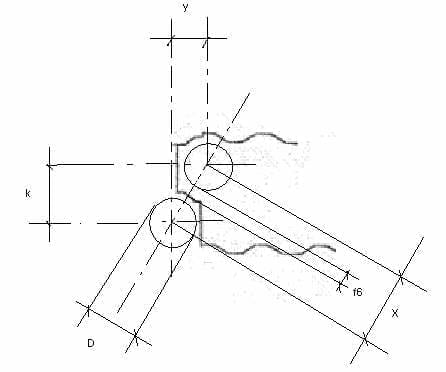
29º.- f6 Para calcular este corte, vamos usar a figura nº 4. Nele é cumprido:
1) y = D/2 + F3 + F4 – F/2
y = 92/2 + 0.8 + 2.25 – 1.1/2 = 48.5
2º) x = V k*k + y*y
x = V 80,624×80,624 + 48,5×48,5 = 94,087
3º) f6 = ( x – D )/ 2
f6 = (94.087 – 92 ) / 2 = 1.0435
Figura 4
30º.- f7. Por um raciocínio análogo ao anterior, nós teríamos:
1º) x’ = V p*p + y*y
x’ = V 81,894×81,894+ 48,5×48,5 = 95,178
3º) f7 = ( x’ – D )/ 2
f6 = (95.178– 92 ) / 2 = 1.589
É possível preparar ou obter um pequeno programa de computador para o cálculo de todos estes valores, sem a necessidade de operar manualmente.











0 comentários