इसे रुचिकर मानते हुए, बॉटम्स के निर्माण के लिए टिन की चादरों और पट्टियों की ज़िगज़ैग कटिंग प्रोफ़ाइल की ज्यामिति की गणना करने का तरीका इस कार्य में विकसित किया गया है।

परिचय

लागत कम करने की आवश्यकता, पिछली शताब्दी के उत्तरार्ध में, कवर और बॉटम के निर्माण के लिए समर्पित धातु की सतह का अधिकतम उपयोग करने की अनिवार्यता को धीरे-धीरे लागू किया जा रहा है। इसके लिए, ज़िग-ज़ैग कट को पहले प्रेस के लिए बैंड में पेश किया गया था, और बाद में, कॉइल से शीट काटने में भी यही तकनीक शुरू की गई थी।

इस कार्य में ज़िग-ज़ैग में इन कटों के सिल्हूट, या प्रोफ़ाइल की गणना के लिए बुनियादी धारणाओं को उजागर करने का प्रयास किया गया है। स्पैनिश में, इस प्रकार की कतरनी को नामित करने के लिए, अंग्रेजी शब्द “स्क्रॉल” कटिंग का उपयोग व्यापक हो गया है। इस कारण से, हम अब से इस शब्द का उपयोग करेंगे। हम प्राइमरी स्क्रॉल कटिंग कहेंगे, जो कॉइल कटिंग लाइनों में बनाई जाती है, और सेकेंडरी स्क्रॉल कटिंग, जो प्रेस के लिए स्ट्रिप्स या बैंड की तैयारी के लिए कैंची पर की जाती है।

हालाँकि स्ट्रिप्स का उपयोग कभी-कभी साधारण डाई के लिए किया जाता है – एक ही पंच के साथ – और इसलिए इसमें बॉटम की केवल एक पंक्ति होती है, सबसे सामान्य मामला डबल डाई के लिए होता है, यानी डबल-पंक्ति बैंड। इसलिए, यह अध्ययन बाद वाले प्रकार पर केंद्रित होगा।

प्रारंभिक पैरामीटर

गणना शुरू करने के लिए, हमें पहले से कुछ डेटा जानना होगा। ये:

– डी = ढक्कन को छिद्रित करने के लिए आवश्यक सामग्री का काटने का व्यास। इसकी गणना और सत्यापन व्यावहारिक रूप से पहले ही किया गया होगा।

– N1 = प्रति बैंड प्राप्त किए जाने वाले कटों की संख्या। हम इन तक सीमित रहेंगे:

– कॉइल स्लाइसिंग लाइन की अधिकतम/न्यूनतम कटिंग पिच।

– स्क्रॉल शीयर द्वारा स्वीकृत शीट की अधिकतम/न्यूनतम चौड़ाई।

– स्ट्रिप की अधिकतम/न्यूनतम लंबाई जिसे प्रेस स्वीकार करता है।

ये डेटा मशीनों के मैनुअल में दर्शाया जाएगा ।

– N2 = बैंड की संख्या जो हम प्रति शीट प्राप्त करना चाहते हैं। यह इसके द्वारा सीमित होगा:

– कॉइल की अधिकतम/न्यूनतम चौड़ाई जिसे कटिंग लाइन स्वीकार करती है।

– शीट की अधिकतम/न्यूनतम लंबाई जिसे स्क्रॉल शीयर स्वीकार करता है।

– F1 = कटों के बीच न्यूनतम कट।

– F2 = बैंड के कट और साइड किनारे के बीच काटें

– F3 = बैंड के कट और सिरे के बीच का कट

– F4 = बैटलमेंट के कट और किनारे के बीच ट्रिम करें

इन कटों का मूल्य प्रेस के काम की सटीकता और डाई की गुणवत्ता से जुड़ा हुआ है।

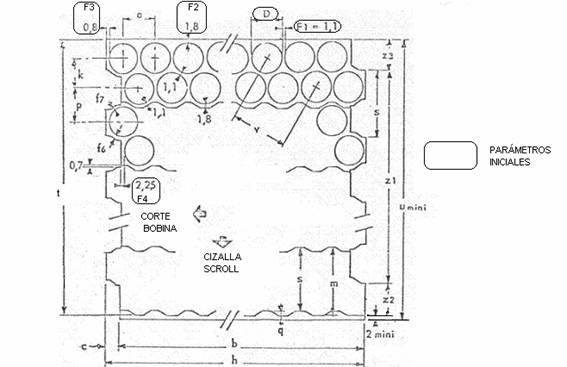
चित्र 1 इन प्रारंभिक मापदंडों को दिखाता है, बेहतर पहचान के लिए उन्हें आयतों में फंसाया गया है।

आइए गणना का बेहतर ढंग से पालन करने के लिए एक उदाहरण रखें,

एक निश्चित सीमा के लिए निम्नलिखित मान मानें:

डी=92मिमी.

एन1 =18 (9 की 2 पंक्तियाँ)

एन2 = 5

F1 = आसन्न कटों के बीच 1.1 मिमी

F2 = कट और बैंड के किनारे के बीच 1.8 मिमी

कट और बैंड सिरे के बीच F3 = 0.8 मिमी

F4 = कट और क्रैनेलेशन के किनारे के बीच 2.25 मिमी

नीचे चित्र 1 देखें. इसमें हमने अक्षरों द्वारा विभिन्न आयामों को दर्शाया है जो कटिंग योजना के विभिन्न मापदंडों को परिभाषित करते हैं।

हमने कॉइल कटिंग और स्क्रॉल शियरिंग के संचालन में सामग्री के आगे बढ़ने की दिशाओं को भी दो तीरों से चिह्नित किया है। अब हम विभिन्न ऊंचाइयों की गणना विकसित करेंगे।

1º.- दो कटों के बीच की दूरी: a = D + F1 ( a = 92 + 1.1 = 93.1 )

यह मान प्रेस में फ़ीड दर से मेल खाता है।

2º.- कुंडल में काटने की लंबाई: b = ax (N1/2 – 1) + D + 2F1

(बी = 93.1 x 18/2 – 1) + 92 + 2 x 0.8 = 838.4)

यह कॉइल कटिंग लाइन का अग्रिम चरण है

3º.- प्राथमिक स्क्रॉल में युद्ध की गहराई: c = a/2 – F3 + F4

(सी = 93.1/2 – 0.8 + 2.25 = 48)

4º.- ब्लेड की लंबाई: एच = बी + सी (एच = 838.4 + 48 = 886.4)

5º.- एक ही बैंड की केंद्र पंक्ति रेखाओं के बीच की दूरी:

के = ए/2 x 1/ टीजी30º

के = 93.1 /2 x 1/ 0.57733 = 80.624

6º.- बैंडविड्थ: एम = 2एफ2 + डी + के (एम = 2 x 1.8 + 92 + 80.624 =176.224)

7º.-दो बैंड की सन्निहित पंक्तियों की केंद्र रेखाओं के बीच की दूरी:

पी = वी (2एफ1 + डी)(2एफ1 +डी) – (एफ1/2 + डी/2) (एफ1/2 + डी/2)

पी = वी (2 x 1.1 + 92 ) (2 x 1.1 + 92 ) – (1.1/2 + 92/2) (1.1/2 + 92/2) = 81.894

8º.- द्वितीयक स्क्रॉल में लड़ाई की ऊंचाई: क्यू = डी + 2एफ2 – पी

(क्यू = 92 + 2 x 1.8 – 81.894 = 13.706)

9º.- स्क्रॉल शीयर में कटिंग चरण : s = m – q ( s = 176.224 -13.706 = 162.518 )

10º.- शीट की शुद्ध चौड़ाई (बिना ट्रिम के): t = (N2 – 1) s + m

टी = (5 -1 ) x 162,518 + 176,224 = 826,296

11º.- न्यूनतम शीट चौड़ाई (कुंडल चौड़ाई) : यू = टी + न्यूनतम ट्रिम

(यू = 826,296 + 2 = 828,296)

यह आंकड़ा गोलाकार है, इसलिए आवश्यक कुंडल चौड़ाई 829 मिमी होगी।

12º.- कवर के लिए डाई में पंचों के केंद्रों के बीच की दूरी।

v = V ( a + D/2 +F1/2) x ( a + D/2 +F1/2) + kxk

वी = वी (93.1 + 92/2 + 1.1/2) एक्स (93.1 + 92/2 + 1.1/2) + 80.624 x 80.624 = 161.252

13º.- चरम युद्धों के बीच की दूरी: z1 = t – m

(z1 = 826,296 -176,224 = 650,072)

14वाँ.- z2 = k ( z2 = 80.624 )

15º.- z3 = t –z1 –z2 ( z3 = 826.296 – 650.072 – 80.624 = 95.6 )

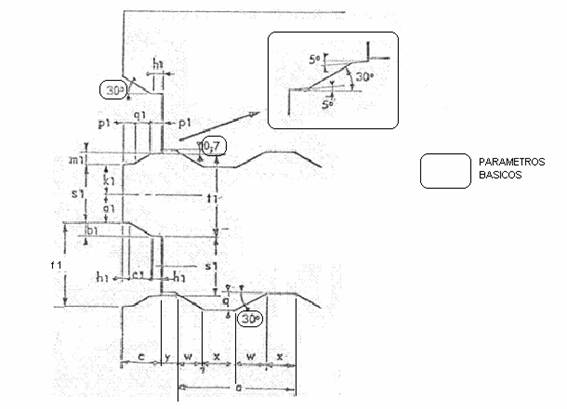
अब तक शीट की मुख्य मापें। अब हम प्राथमिक और द्वितीयक स्क्रॉल की लड़ाइयों की प्रोफाइल की विस्तृत माप की परिभाषा में प्रवेश करते हैं। ऐसा करने के लिए, हम चित्र 2 में परिभाषित आयामों का पालन करेंगे।

बुनियादी पैरामीटर:

-ए) प्राथमिक और द्वितीयक स्क्रोल दोनों में युद्धपोतों में ढलान का कोण 30º है।

-बी) प्राथमिक के बैटलमेंट के शीर्ष के संबंध में, द्वितीयक स्क्रॉल के कट की शुरुआत का विस्थापन 0.7 मिमी है। यह सुनिश्चित करता है कि कट साफ होगा, किनारों पर कांटे नहीं बनेंगे।

-सी) उसी पिछले प्रभाव को सुविधाजनक बनाने के लिए, प्राथमिक स्क्रॉल के बैटलमेंट का ढलान, माध्यमिक के कट के साथ मेल खाते हुए, एक मिश्रित ढलान है, जिसमें दो झुकाव 5º और 30º हैं। चित्र क्रमांक 2 का विवरण देखें

चित्रा संख्या 2

16º.- द्वितीयक स्क्रॉल के युद्धपोत की लंबित लंबाई: w = q /tg 30º

(डब्ल्यू = 13.706 /0.57733 = 23.74)

17वां. सेकेंडरी स्क्रॉल बैटलमेंट बेस लंबाई: x = (a – 2w)/2

(x = (93.1 – 2 x 23.74)/2 = 22.81)

18वाँ.- a1 = k – D/2 – F2 ( a1 = 80.624 – 92/2 – 1.8 = 32.824 )

19वाँ.- b1 = k – 2 a1 ( b1 = 80.624 – 2 x 32.824 = 14.976 )

20º.- c1 = b1/ tg30º ( c1 = 14.976/0.5773 = 25.94 )

21º.- h1 = ( c – c1 )/2 h1 = ( 48 – 25.94 )/2 = 11.03

22वां.- के1 = पी – डी/2 – एफ2 + 0.7 ( के1 = 81.894 – 46 – 1.8 + 0.7 = 34.794 )

23वां- एम1 = पी – 2के1 (एम1 = 81,894 – 2 x 34,794 = 12,306)

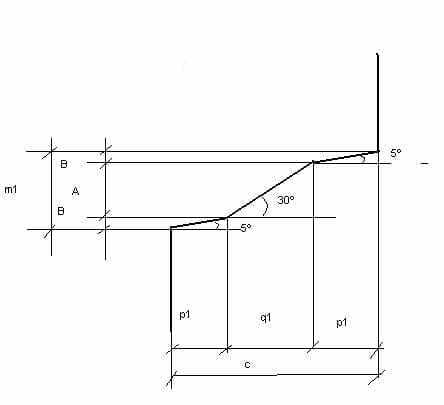
24º और 25º.- आयाम p1 और q1 की गणना करने के लिए हम चित्र 3 को देखेंगे।

इसमें निम्नलिखित समीकरण पूरा होता है:

सी = 2पी1 + क्यू1

m1 = 2B + A, B = p1 x tg 5º , A = q1 x tg 30º

इसलिए m1 = 2p1 x tg5º + q1 x tg30º = 0.176 p1 + 0.5773 q1

इसलिए दो अज्ञातों का समीकरण इस प्रकार उठाया गया है:

सी = 2पी1 + क्यू1

एम1 = 0.176पी1 + 0.5773 क्यू1

लेकिन चूँकि c और m1 पहले से ही ज्ञात मान हैं, हमारे पास यह होगा:

2पी1 + क्यू1 = 48

0.176पी1 + 0.5773 क्यू1 = 12.306

इस अभिव्यक्ति को हल करने से हमें निम्नलिखित मान प्राप्त होते हैं:

पी1 = 15.741 क्यूएल = 16.518

26º.- ऊंचाई की गणना और:

चित्र 2 में यह पूरा हुआ है कि:

c + y + w – p1 = w + x + w, सरलीकरण:

c + y – p1 = w + x, कहाँ से:

y = w + x + p1 – c

y = 23.74 + 22.81 + 15.741 – 48 = 14.291

27º.- s1 = k1 + a1 ( s1 = 34.794 + 32.824 = 67.618 )

28º.- एफ1 = एम1 + एस1 + बी1 (एफ1 = 12.306 + 67.618 + 14.976 = 94.9)

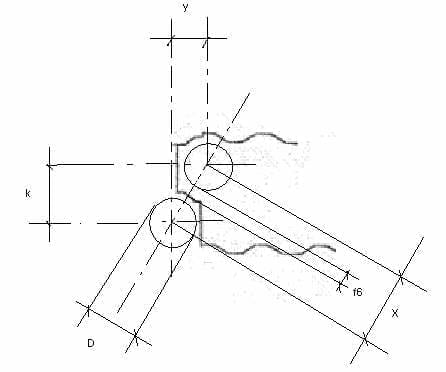
29º.- f6 इस कटौती की गणना करने के लिए, हम चित्र 4 पर भरोसा करेंगे। इसमें पूरा किया गया है:

पहला) y = D/2 + F3 + F4 – F/2

y = 92/2 + 0.8 + 2.25 – 1.1/2 = 48.5

2º) x = V k*k + y*y

एक्स = वी 80.624×80.624 + 48.5×48.5 = 94.087

3º) f6 = (x – D )/ 2

एफ6 = ( 94.087 – 92) / 2 = 1.0435

चित्र संख्या 4

30º.- f7 . पिछले तर्क के समान तर्क से हमारे पास यह होगा:

1º) x´ = V p*p + y*y

x´ = वी 81.894×81.894+ 48.5×48.5 = 95.178

3º) f7 = (x´ – D )/ 2

एफ6 = ( 95.178-92)/2 = 1.589

हाथ से संचालित करने की आवश्यकता के बिना, इन सभी मूल्यों की गणना करने के लिए एक छोटा कंप्यूटर प्रोग्राम तैयार करना या प्राप्त करना संभव है।

मुंडो लतास प्रक्रिया को लौटें