हम कंटेनरों के निरीक्षण में लागू चर द्वारा गुणवत्ता नियंत्रण प्रणाली में उपयोग की जाने वाली प्रत्येक बुनियादी अवधारणा को बहुत सरल तरीके से परिभाषित करने जा रहे हैं।

इससे पहले कि हम परिभाषित करें कि चर से हमारा क्या तात्पर्य है।

हम किस प्रकार के चरों को जानते हैं?
विचार करने के लिए दो प्रकार के चर हैं, सतत चर और असतत चर।

सतत चर
सतत चर वे होते हैं जिन्हें मापा जाता है।
असतत चर
अलग-अलग चरों की गणना की जाती है।
पहला चर द्वारा नियंत्रण को जन्म देता है और दूसरा विशेषताओं द्वारा नियंत्रण को जन्म देता है।

गुणवत्ता विशेषताएँ जिन्हें हम चर कहेंगे वे सभी वे हैं जिन्हें एक संख्या द्वारा दर्शाया जा सकता है। उदाहरण के लिए, बोल्ट का आकार, तार प्रतिरोधकों का प्रतिरोध, कोयले में राख की मात्रा आदि।
विशेषताएँ वे गैर-मापने योग्य गुणवत्ता विशेषताएँ हैं, जिनके आयाम को सामान्यतः किसी संख्या के साथ प्रदर्शित नहीं किया जा सकता है। उदाहरण के तौर पर हम उत्पादों की सतहों की दृश्य खामियां ले सकते हैं, जैसे धब्बे, टोन में अंतर, वेल्ड के पहलू इत्यादि।
अंत में, हमें यह ध्यान में रखना चाहिए कि प्रक्रियाओं और तैयार बैचों दोनों का निरीक्षण विशेषताओं या चर द्वारा किया जा सकता है।

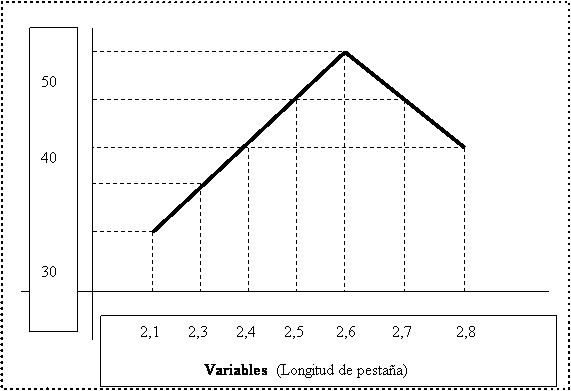
सबसे अच्छा तरीका व्यावहारिक उदाहरण का उपयोग करना है। मान लीजिए कि हम कंटेनर बॉडी फ्लैंज की लंबाई को नियंत्रित कर रहे हैं। मापों की एक श्रृंखला के बाद हम उनके साथ एक ग्राफ़ बनाते हैं जैसा चित्र 1 में दर्शाया गया है। हम एब्सिस्सा पर टैब की लंबाई और कोर्डिनेट पर कंटेनरों की संख्या के लिए पाए गए मान लेते हैं।

इस ग्राफ़ को ध्यान में रखते हुए हम इसे इस प्रकार परिभाषित करेंगे:

चर : मापा जाने वाला पैरामीटर. इस मामले में टैब की लंबाई.

आवृत्ति : किसी चर को दोहराए जाने की संख्या। हमारे उदाहरण में कंटेनरों की संख्या.

भ्रमण: वह सीमा जिसमें कोई चर चलता है। 2.1 और 2.8 मिमी के बीच (निकला हुआ किनारा लंबाई मान)

अंतराल : एक निश्चित पथ के भीतर एक चर के मानों का समूहन। उदाहरण के लिए: 2.3 और 2.4 के बीच के सभी मानों को मान 2.4 में समूहित करना।

आयाम : मार्ग के चरम मूल्यों के बीच अंतर. हमारे लैश उदाहरण में: 2.8 – 2.1 = 0.7 चौड़ाई।

माध्य: (या अंकगणितीय माध्य): डेटा की कुल संख्या से विभाजित सभी मानों का योग

एक्स = (10*2.1 + 20*2.3 + 30*2.4 + 40*2.5 + 50*2.6 + 40*2.7 + 30*2.8) / (10 + 20 + 30 + 40 + 50 + 40 + 30 ) = (21 + 46 + 72 + 100 + 130 + 108 + 84) / 220 = 2.55

माध्यिका: वितरण का मान, यह मानते हुए कि इसे निम्नतम से उच्चतम की ओर क्रमबद्ध किया गया है, बाईं और दाईं ओर समान संख्या में आवृत्तियों को छोड़कर, अर्थात, वह मान जो केंद्रीय स्थान पर है, डेटा की विषम संख्या मानते हुए। यदि डेटा की संख्या सम होती, तो यह कहा जा सकता है कि दो माध्यिका मान हैं और उनके बीच अंकगणितीय माध्य लिया गया है।

टैब की लंबाई के पिछले उदाहरण को जारी रखते हुए हमारे पास होगा:

आवृत्तियाँ = 10 + 20 + 30 + 40 + 50 + 40 + 30 = 220

220 पूर्ण या संचित आवृत्ति होगी

आवृत्ति का केंद्र = 220/2 = 110

इसलिए, माध्यिका होगी: 2.6 , क्योंकि यह उस चर का मान है जो शुरुआत से शुरू होकर 110वें स्थान पर है।

आवृत्ति संचयी आवृत्ति चर (एम/एम )

10 10 2,1

20 30 2,3

30 60 2,4

40 100 2,5

50 150 2,6

40 190 2,7

30 220 2,8

इसमें अधिक जानकारी:

http://html.rincondelvago.com/control-de-calidad-estadistico.html

मुंडो लतास को नियंत्रित करने के लिए वापस