Da es als interessant erachtet wird, wird in dieser Arbeit die Art und Weise der Berechnung der Geometrie des Zickzack-Schnittprofils von Blechen und Streifen aus Weißblech entwickelt, die für die Herstellung von Böden bestimmt sind.

EINLEITUNG

In der zweiten Hälfte des letzten Jahrhunderts hat die Notwendigkeit, die Kosten zu senken, nach und nach dazu geführt, dass die Metalloberfläche, die für die Herstellung von Deckeln und Böden vorgesehen ist, optimal genutzt wird. Zu diesem Zweck wurde das Zick-Zack-Schneiden zunächst für Pressenbahnen eingeführt, später wurde die gleiche Technik zum Schneiden von Bögen von Coils verwendet.

Ziel dieser Arbeit ist es, die Grundbegriffe für die Berechnung der Silhouette bzw. des Profils dieser Zick-Zack-Schnitte darzustellen. Im Spanischen hat sich zur Bezeichnung dieser Art des Scherens der Gebrauch des englischen Wortes „scroll shearing“ durchgesetzt. Daher werden wir diesen Begriff von nun an verwenden. Als primäres Schneiden bezeichnen wir das Schneiden auf den Coil-Schneideanlagen und als sekundäres Schneiden das Schneiden auf den Scheren für die Vorbereitung von Bändern oder Streifen für Pressen.

Obwohl Streifen manchmal für einzelne Matrizen – Einzelstempel – verwendet werden und daher nur eine Reihe von Böden enthalten, ist der üblichste Fall der für doppelte Matrizen, d.h. zweireihige Streifen. Diese Studie wird sich daher auf den letzteren Typ konzentrieren.

GRUNDEINSTELLUNGEN

Um die Berechnung zu starten, müssen wir vorher einige Daten kennen. Diese sind:

– D = Der Schnittdurchmesser des Materials, das zum Stanzen des Deckels benötigt wird. Sie muss vorher berechnet und praktisch überprüft worden sein.

– N1 = Anzahl der zu erzielenden Schnitte pro Band. Wir werden begrenzt durch:

– die maximale/minimale Schneidenteilung der Bandspaltanlage.

– die maximale/minimale Blechbreite, die von der Rollenschere zugelassen wird.

– die maximale/minimale Bandlänge, die die Presse akzeptiert.

Diese Daten werden in den Handbüchern der Maschinen angegeben.

– N2 = Anzahl der Bänder, die wir pro Blatt erhalten möchten. Es wird begrenzt durch:

– die maximale Breite/Minute des Coils, die die Spaltanlage verarbeiten kann.

– die maximale/minimale Blechlänge, die die Rollenschere verarbeiten kann.

– F1 = Minimaler Beschnitt zwischen den Schnitten.

– F2 = Beschneiden zwischen Schnitt und Seitenkante des Bandes

– F3 = Trimmen zwischen Schnitt und Bandende

– F4 = Beschnitt zwischen Schnitt und Zinnenkante

Der Wert dieser Zuschnitte hängt von der Arbeitsgenauigkeit der Presse und der Qualität des Werkzeugs ab.

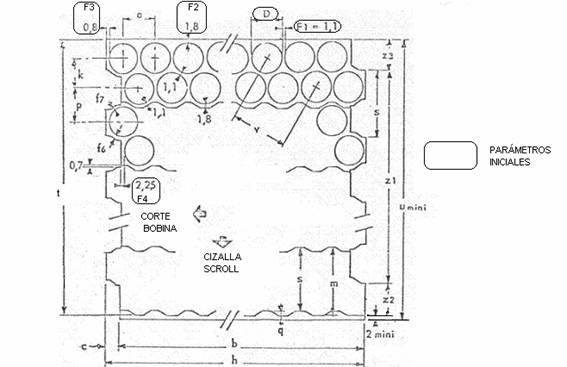
Abbildung 1 zeigt diese Ausgangsparameter, zur besseren Identifizierung sind sie in Rechtecken eingerahmt.

Lassen Sie uns ein Beispiel geben, um die Berechnung besser nachvollziehen zu können,

Nehmen Sie die folgenden Werte für eine bestimmte Kappe an:

D = 92 mm.

N1 =18 ( 2 Reihen à 9)

N2 = 5

F1 = 1,1 mm zwischen zusammenhängenden Scheiben

F2 = 1,8 mm zwischen Schnitt und Seitenkante der Leiste

F3 = 0,8 mm zwischen Schnitt und Bandende

F4 = 2,25 mm zwischen Schnitt und Zinnenkante

Siehe Abbildung Nr. 1 unten. Darin haben wir durch Buchstaben die verschiedenen Dimensionen dargestellt, die die verschiedenen Parameter des Schneideschemas definieren.

Außerdem haben wir mit zwei Pfeilen die Materialvorschubrichtungen bei den Arbeitsgängen Coilschneiden und Schneiden mit der Schere markiert. Wir werden nun die Berechnung der verschiedenen Dimensionen entwickeln.

1º.- Abstand zwischen zwei Schnitten: a = D + F1 ( a = 92 + 1,1 = 93,1 )

Dieser Wert a entspricht der Vorschubgeschwindigkeit in der Presse.

2º.- Spulenschnittlänge: b = a x (N1/2 – 1) + D + 2F1

( b = 93,1 x 18/2 – 1) + 92 + 2 x 0,8 = 838,4 )

Es ist der Vorschubschritt an der Coil-Schneidanlage.

3º.- Tiefe der Zinnenbildung in der primären Schnecke: c = a/2 – F3 + F4

( c = 93.1/2 – 0.8 + 2.25 = 48 )

4º.- Blattlänge: h = b + c ( h = 838,4 + 48 = 886,4 )

5º.- Abstand zwischen den Mittelreihen desselben Kissens:

k = a/2 x 1/ tg30º k = a/2 x 1/ tg30º k = a/2 x 1/ tg30º

k = 93,1 /2 x 1/ 0,57733 = 80,624

6º.- Bandbreite : m = 2F2 + D + k ( m = 2 x 1,8 + 92 + 80,624 =176,224 )

7º.-Abstand zwischen den Mittellinien zweier aneinandergrenzender Reihen von zwei Polstern:

p = V (2F1 + D)(2F1 + D) – (F1/2 + D/2) (F1/2 + D/2)

p = V (2 x 1,1 + 92 ) (2 x 1,1 + 92 ) – (1,1/2 + 92/2) (1,1/2 + 92/2) = 81,894

8º.- Höhe der Zinne in der Nebenschnecke: q = D + 2F2 – p

( q = 92 + 2 x 1,8 – 81,894 = 13,706 )

9º.- Scherschritt in der Schneckenschere: s = m – q ( s = 176,224 -13,706 = 162,518 )

10º.- Netto-Bogenbreite (ohne Beschnitt): t = ( N2 – 1 ) s + m

t = (5 -1 ) x 162,518 + 176,224 = 826,296

11º.- Minimale Blechbreite (Coilbreite) : u = t + minimaler Beschnitt

( u = 826.296 + 2 = 828.296 )

Diese Zahl wird aufgerundet, so dass 829 mm die erforderliche Spulenbreite wäre.

12º.- Abstand zwischen den Stempelmitten in den Kappenmatrizen.

v = V ( a ( a + D/2 +F1/2) x ( a + D/2 +F1/2) + k x k

v = V ( 93,1 + 92/2 + 1,1/2 ) x ( 93,1 + 92/2 + 1,1/2 ) + 80,624 x 80,624 = 161,252

13º.- Abstand zwischen den äußersten Zinnen: z1 = t – m

( z1 = 826.296 -176.224 = 650.072)

14º.- z2 = k ( z2 = 80.624 )

15º.- z3 = t -z1 -z2 ( z3 = 826,296 – 650,072 – 80,624 = 95,6 )

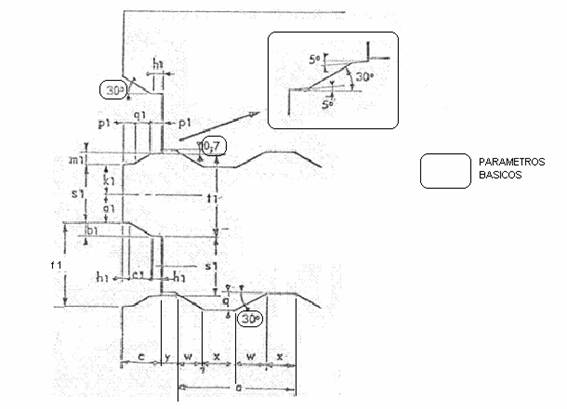
Soweit die Hauptmessungen des Blattes. Wir gehen nun in die Definition der detaillierten Messungen der primären und sekundären Schneckenzackenprofile über. Dazu folgen wir den in Abbildung Nr. 2 definierten Abmessungen.

Grundlegende Parameter:

A) Der Neigungswinkel auf den Zinnen, sowohl der primären als auch der sekundären Schnecke, beträgt 30º.

B) Die Verschiebung des Schnittanfangs der sekundären Schnecke, bezogen auf den Scheitelpunkt der primären Schneckenzone, beträgt 0,7 mm. Dadurch wird sichergestellt, dass der Schnitt sauber ist und keine Dornen an den Rändern entstehen.

C) Um den gleichen Effekt wie oben zu erzielen, hat die Neigung der primären Schnecke, die mit der Abschaltung der sekundären Schnecke zusammenfällt, eine zusammengesetzte Neigung, mit zwei Neigungen von 5º und 30º. Siehe Detail in Abbildung Nr. 2

Abbildung 2

16º.- Schräglänge der sekundären Schneckenzelle: w = q /tg 30º.

(w = 13.706 /0.57733 = 23.74 )

17º. Basislänge der Sekundärspirale: x = ( a – 2w )/2

(x = (93,1 – 2 x 23,74)/2 = 22,81)

18º.- a1 = k – D/2 – F2 ( a1 = 80,624 – 92/2 – 1,8 = 32,824 )

19º.- b1 = k – 2 a1 ( b1 = 80,624 – 2 x 32,824 = 14,976 )

20º.- c1 = b1/ tg30º ( c1 = 14,976/0,5773 = 25,94 )

21º.- h1 = ( c – c1 )/2 h1 = ( 48 – 25,94 )/2 = 11,03

22º.- k1 = p – D/2 – F2 + 0,7 ( k1 = 81,894 – 46 – 1,8 + 0,7 = 34,794 )

23º.- m1 = p – 2k1 ( m1 = 81,894 – 2 x 34,794 = 12,306 )

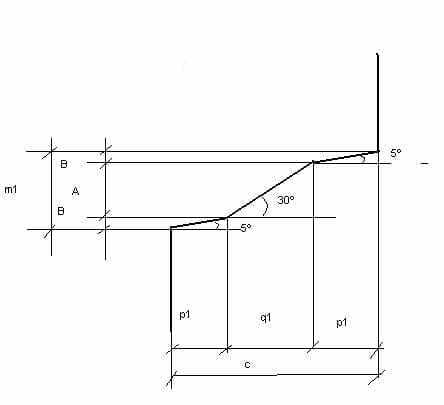
24º und 25º.- Um die Koordinaten p1 und q1 zu berechnen, betrachten wir die Abbildung Nr. 3.

Darin wird die folgende Gleichung erfüllt:

c = 2p1 + q1

m1 = 2B + A, B = p1 x tg 5º , A = q1 x tg 30º.

Daher m1 = 2p1 x tg5º + q1 x tg30º = 0,176 p1 + 0,5773 q1

Daher wird die Gleichung mit zwei Unbekannten wie folgt angegeben:

c = 2p1 + q1

m1 = 0,176p1 + 0,5773 q1

aber da c und m1 bereits bekannte Werte sind, würden wir haben:

2p1 + q1 = 48

0,176p1 + 0,5773 q1 = 12,306

Wenn wir diesen Ausdruck lösen, erhalten wir die folgenden Werte:

p1 = 15,741 ql = 16,518

26º.- Berechnung der y :

In der Abbildung Nr. 2 ist das erfüllt:

c + y + w – p1 = w + x + w, vereinfachend:

c + y – p1 = w + x, woraus folgt:

y = w + x + p1 – c

y = 23.74 + 22.81 + 15.741 – 48 = 14.291

27º.- s1 = k1 + a1 ( s1 = 34,794 + 32,824 = 67,618 )

28º.- f1 = m1 + s1 + b1 ( f1 = 12.306 + 67.618 + 14.976 = 94.9 )

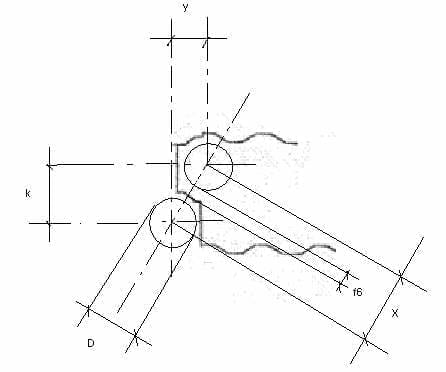
29º.- f6 Um diesen Schnitt zu berechnen, verwenden wir Abbildung Nr. 4. Darin ist sie erfüllt:

1.) y = D/2 + F3 + F4 – F/2

y = 92/2 + 0.8 + 2.25 – 1.1/2 = 48.5

2º) x = V k*k + y*y

x = V 80,624×80,624 + 48,5×48,5 = 94,087

3º) f6 = ( x – D )/ 2

f6 = (94.087 – 92 ) / 2 = 1.0435

Abbildung 4

30º.- f7. Durch eine analoge Argumentation zur vorherigen hätten wir:

1º) x‘ = V p*p + y*y

x‘ = V 81,894×81,894+ 48,5×48,5 = 95,178

3º) f7 = ( x‘ – D )/ 2

f6 = (95.178– 92 ) / 2 = 1.589

Es ist möglich, ein kleines Computerprogramm für die Berechnung all dieser Werte vorzubereiten oder zu erhalten, ohne dass Sie von Hand arbeiten müssen.

Zurück zu Can World Prozess