ここでは、品質管理システムで使用される基本的な概念のそれぞれを、包装の検査に適用される変数によって、非常にわかりやすく定義していきます。

まず、変数という意味を定義しておこう。

どのような変数がわかっているのか？
変数には「連続変数」と「離散変数」の2種類があります。

連続変数
連続変数とは、測定される変数のことである。
離散変数
離散変数がカウントされます。
前者は変数による制御を、後者は属性による制御を生み出す。

これから変数と呼ぶ品質特性は、すべて数値で表すことができるものである。 例：ボルトのサイズ、電線抵抗の抵抗値、炭素中の灰分などなど。
属性とは、一般に数値で表すことのできない非測定的な品質特性のことで、その次元を表す。 例えば、製品表面の汚れ、濃淡の違い、溶接の様子など、視覚的な欠点を取ることができます。
最後に、プロセスも完成バッチも、属性や変数によって検査できることに留意する必要がある。

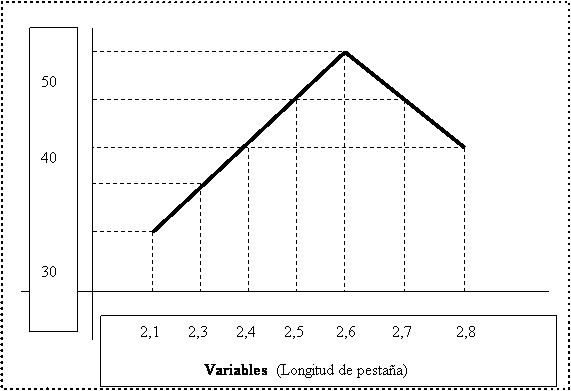
一番いい方法は、実例を使ってみることです。 例えば、容器本体のフランジの長さを制御するとします。 一連の測定が終わると、図1のようなグラフを作成する。 横軸にフランジ長さ、縦軸に容器の個数をとっています。

このグラフを見ながら、どのようにするかを定義していきます。

変数：測定されるパラメータ。 この場合は、まつ毛の長さです。

頻度：ある変数が繰り返される回数。 この例では、コンテナの数です。

パス：変数が移動する範囲。 2.1～2.8mm間（フランジ長値）

区間：ある範囲内の変数の値のグループ化。 例：2.3～2.4の値をすべて2.4という値にグループ化する。

振幅: パスの極値間の差。 まつ毛の例では、2.8 – 2.1 = 0.7 振幅です。

平均：（または算術平均）：すべての値の合計をデータの総数で割ったもの。

X = (10*2.1 + 20*2.3 + 30*2.4 + 40*2.5 + 50*2.6 + 40*2.7 + 30*2.8) / (10 + 20 + 30 + 40 + 50 + 40 + 30 ) = ( 21 + 46 + 72 + 100 + 130 + 108 + 84) / 220 = 2.55

中央値：分布が小さいものから大きいものへと順番に並んでいると仮定し、その左右の度数が同じである値、すなわちデータが奇数であると仮定した場合に中央の位置を占める値です。 データ数が偶数であれば、中央値が2つあり、その間の算術平均をとっているといえる。

先ほどのフランジの長さの例から続けると、次のようになります。

周波数＝10＋20＋30＋40＋40＋50＋40＋30＝220

220は、絶対頻度または累積頻度

中心周波数＝220÷2＝110

したがって、中央値はそうなる。
2.6
というのは，これが先頭から 110 番目を占める変数の値だからです。

頻度 累積頻度 変数(m/m)

10 10 2,1

20 30 2,3

30 60 2,4

40 100 2,5

50 150 2,6

40 190 2,7

30 220 2,8

詳細については、以下をご覧ください。

http://html.rincondelvago.com/control-de-calidad-estadistico.html

キャンワールドコントロールに戻る