بالنظر إلى الاهتمام ، يطور هذا العمل كيفية حساب هندسة التشكيل الجانبي المقطوع المتعرج للصفائح وشرائح من الصفيح لتصنيع الخلفيات.

المقدمة

لقد أدت الحاجة إلى خفض التكاليف تدريجياً ، في النصف الثاني من القرن الماضي ، إلى ضرورة تحقيق أقصى استفادة من السطح المعدني المخصص لتصنيع الأغطية والقيعان. للقيام بذلك ، تم إدخال القطع المتعرج أولاً في شرائط المكبس ، وبعد ذلك ، تم إدخال نفس التقنية في قص الألواح من البكرات.

الهدف من هذا العمل هو تقديم المفاهيم الأساسية لحساب الصورة الظلية أو المظهر الجانبي لهذه التخفيضات المتعرجة. في اللغة الإسبانية ، لتعيين هذا النوع من القص ، أصبح استخدام الكلمة الإنجليزية “التمرير” واسع الانتشار. لذلك ، سوف نستخدم هذا المصطلح من الآن فصاعدًا. سوف نسمي القطع التمرير الأساسي ، الذي يتم تنفيذه في خطوط تقطيع الملف ، ويقوم التمرير الثانوي بقطع التمرير الذي تم إجراؤه على المقصات لإعداد الشرائط أو العصابات للمكابس.

على الرغم من استخدام الأشرطة أحيانًا للقوالب البسيطة – بكمة واحدة – وبالتالي تحتوي على صف واحد فقط من الخلفيات ، فإن الحالة الأكثر شيوعًا هي تلك المخصصة للقوالب المزدوجة ، أي نطاقات الصف المزدوج. لذلك ستركز هذه الدراسة على النوع الأخير.

المعلمات الأولية

لبدء الحساب ، يجب أن نعرف مسبقًا بعض البيانات. هؤلاء هم:

– د = قطر القطع للمادة اللازمة لكمة الغطاء. يجب أن يكون قد تم حسابه مسبقًا والتحقق منه من الناحية العملية.

– N1 = عدد القطع التي سيتم الحصول عليها لكل نطاق. ستقتصر على:

– الحد الأقصى / الحد الأدنى لخطوة القطع لخط تقطيع الملف.

– أقصى / أدنى عرض للورقة مدعوم بقص التمرير.

– الحد الأقصى / الأدنى لطول الشريط الذي ستدعمه الصحافة.

سيتم الإشارة إلى هذه البيانات في أدلة الآلات .

– N2 = عدد النطاقات التي نريد الحصول عليها لكل ورقة. ستكون مقيدًا بـ:

– الحد الأقصى / الأدنى لعرض الملف الذي يدعمه خط القطع.

– الحد الأقصى / الأدنى لطول الورقة الذي يمكن أن يقبله مقص التمرير.

– F1 = الحد الأدنى من القص بين الجروح.

– F2 = تقليم بين الحافة المقطوعة والجانبية للحزام

– F3 = تقليم بين قطع ونهاية الحزام

– F4 = تقليم بين قطع حافة الحافة

ترتبط قيمة هذه التخفيضات بدقة الصحافة وجودة القالب.

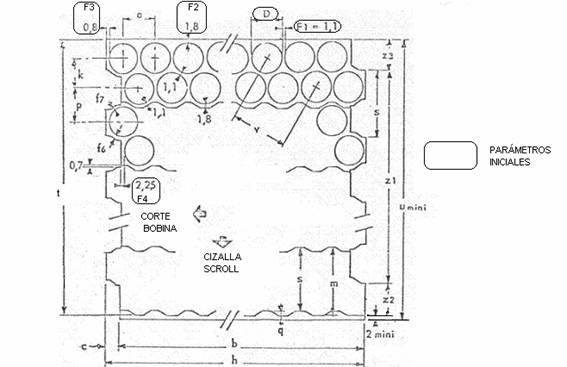
في الشكل 1 ، يشار إلى هذه المعلمات الأولية ، من أجل تحديد أفضل ، تم تأطيرها في مستطيلات.

دعنا نستعرض مثالًا لمتابعة الحساب بشكل أفضل ،

افترض القيم التالية لسقف معين:

D = 92 ملم.

N1 = 18 (صفان من 9)

N2 = 5

F1 = 1.1 مم بين القطع المتجاورة

F2 = 1.8 مم بين حافة الشريط المقطوع والجانبي

F3 = 0.8 مم بين نهاية القطع والشريط

F4 = 2.25 مم بين القطع وحافة الحافة

انظر الشكل رقم 1 أدناه. لقد مثلنا فيه بالحروف الأبعاد المختلفة التي تحدد المعلمات المختلفة لمخطط القطع.

لقد حددنا أيضًا بسهمين ، اتجاهات تقدم المواد في عمليات قطع الملف ، وقص التمرير. سنقوم الآن بتطوير حساب الأبعاد المختلفة.

1º. – المسافة بين قطعتين: أ = D + F1 (أ = 92 + 1.1 = 93.1)

هذه القيمة إلى يتوافق مع الخطوة المتقدمة في الصحافة.

2º. – طول القطع في الملف: ب = الفأس (N1 / 2-1) + D + 2F1

(ب = 93.1 × 18 / 2-1) + 92 + 2 × 0.8 = 838.4)

إنها الخطوة المتقدمة في خط قطع الملف

3º. – عمق المعارك في التمرير الأساسي: ج = أ / 2 – F3 + F4

(ج = 93.1 / 2 – 0.8 + 2.25 = 48)

4.- طول النصل: ح = ب + ج (ع = 838.4 + 48 = 886.4)

5º. – المسافة بين خطوط الصف الأوسط من نفس النطاق:

ك = أ / 2 × 1 / tg30º

ك = 93.1 / 2 × 1 / 0.57733 = 80.624

6 – عرض النطاق الترددي: م = 2F2 + D + ك (م = 2 × 1.8 + 92 + 80.624 = 176.224)

7.-المسافة بين خطوط مركز الصف المتجاورة لنطاقين:

ع = V (2F1 + D) (2F1 + D) – (F1 / 2 + D / 2) (F1 / 2 + D / 2)

ع = V (2 × 1.1 + 92) (2 × 1.1 + 92) – (1.1 / 2 + 92/2) (1.1 / 2 + 92/2) = 81.894

8º. – ارتفاع الشرفة في التمرير الثانوي: ف = د + 2F2 – ص

(ف = 92 + 2 × 1.8 – 81894 = 13706)

9º. – خطوة القطع في القص التمرير : s = m – q (ق = 176،224 -13،706 = 162،518)

10º. – العرض الصافي للورقة (بدون تقليم): ر = (N2 – 1) ث + م

ر = (5 -1) × 162.518 + 176.224 = 826296

11º. – الحد الأدنى لعرض الورقة (عرض الملف) : u = t + الحد الأدنى من القطع

(ش = 826.296 + 2 = 828.296)

تم تقريب هذا الرقم ، لذلك سيكون 829 مم هو عرض الملف المطلوب

12º. – تموت المسافة بين مراكز اللكمات في القبعات.

ت = V (أ + د / 2 + F1 / 2) × (أ + د / 2 + F1 / 2) + ككسك

الخامس = V (93.1 + 92/2 + 1.1 / 2) × (93.1 + 92/2 + 1.1 / 2) + 80.624 × 80.624 = 161.252

13º. – المسافة بين المعارك المتطرفة: z1 = t – م

(z1 = 826.296 -176.224 = 650.072)

الرابع عشر. – z2 = ك (z2 = 80.624)

15º.- z3 = t –z1 –z2 (z3 = 826.296 – 650.072 – 80.624 = 95.6)

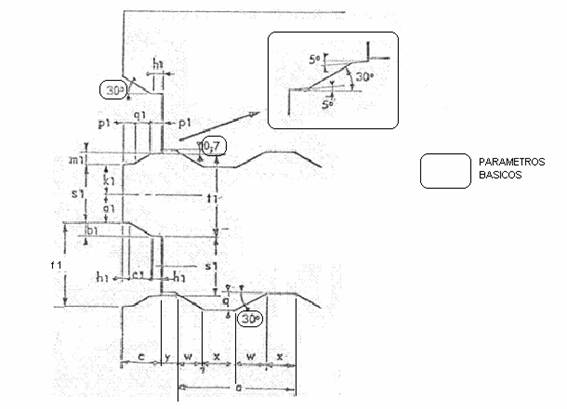
حتى الآن القياسات الرئيسية للورقة. ندخل الآن في تعريف القياسات التفصيلية لمحات عن أسوار اللفائف الأولية والثانوية. للقيام بذلك سوف نتبع الأبعاد المحددة في الشكل 2.

المعلمات الأساسية:

-أ) زاوية المنحدر في الأسوار ، سواء التمرير الابتدائي والثانوي ، 30 درجة.

-ب) يبلغ إزاحة بداية القطع لللفائف الثانوية ، فيما يتعلق برأس الحاجز الأساسي ، 0.7 مم. هذا يضمن أن يكون القطع نظيفًا ، ولا ينتج عنه أشواك على الحواف.

-C) لتسهيل نفس التأثير السابق ، فإن منحدر قاعدة التمرير الأساسي ، بالتزامن مع قطع التمرير الثانوي ، له منحدر مركب ، بميلان 5º و 30º. انظر تفاصيل الشكل رقم 2

الشكل رقم 2

السادس عشر. – طول المنحدر لعربة التمرير الثانوية: ث = q / tg 30º

(ث = 13.706 / 0.57733 = 23.74)

17. طول قاعدة الشرفة من التمرير الثانوي: س = (أ – 2 واط) / 2

(س = (93.1 – 2 × 23.74) / 2 = 22.81)

الثامن عشر. – a1 = ك – د / 2 – F2 (a1 = 80،624 – 92/2 – 1.8 = 32،824)

19 – ب 1 = ك – 2 أ 1 (ب 1 = 80.624 – 2 × 32824 = 14976)

العشرون. – c1 = b1 / tg30º (ج 1 = 14.976 / 0.5773 = 25.94)

21º. – h1 = (c – c1) / 2 ح 1 = (48 – 25.94) / 2 = 11.03

22º.- k1 = p – D / 2 – F2 + 0.7 (ك 1 = 81.894 – 46 – 1.8 + 0.7 = 34.794)

23º.- م 1 = ص – 2 ك 1 (م 1 = 81894 – 2 × 34794 = 12306)

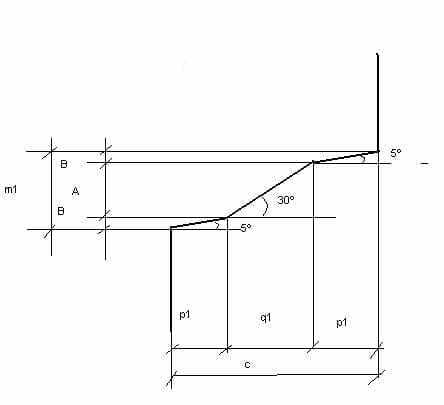
الرابع والعشرون والخامس والعشرون. – لحساب الارتفاعات ص 1 ص q1 سننظر في الشكل 3.

في ذلك ، يتم استيفاء المعادلة التالية:

ج = 2p1 + q1

m1 = 2B + A، B = p1 x tg 5º، A = q1 x tg 30º

لذلك m1 = 2p1 x tg5º + q1 x tg30º = 0.176 p1 + 0.5773 q1

لذلك ، فإن معادلة المجهولين تنص على ما يلي:

ج = 2p1 + q1

م 1 = 0.176 ع 1 + 0.5773 ربع أول

ولكن كيف ج و m1 هي قيم معروفة بالفعل ، سيكون لدينا:

2p1 + q1 = 48

0.176p1 + 0.5773 q1 = 12.306

إذا حللنا هذا التعبير فإنه يعطينا القيم التالية:

p1 = 15،741 ql = 16،518

26º. – حساب الارتفاع ص:

في الشكل رقم 2 ، تحقق ما يلي:

c + y + w – p1 = w + x + w ، التبسيط:

c + y – p1 = w + x ، ومن أين:

ص = ث + س + ص 1 – ج

ص = 23.74 + 22.81 + 15.741 – 48 = 14.291

السابع والعشرون – s1 = k1 + a1 (s1 = 34794 + 32824 = 67618)

28. – f1 = m1 + s1 + b1 (f1 = 12.306 + 67.618 + 14.976 = 94.9)

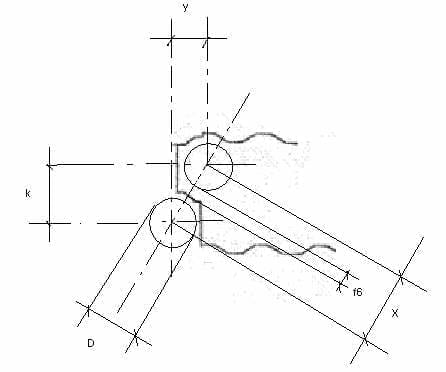
29º.- و 6 لحساب هذا الخفض ، سنستخدم الشكل 4. فيه تتحقق:

الأول) ص = د / 2 + F3 + F4 – و / 2

ص = 92/2 + 0.8 + 2.25 – 1.1 / 2 = 48.5

الثاني) x = V k * k + y * y

x = V 80.624×80.624 + 48.5×48.5 = 94.087

الثالث) f6 = (س – د) / 2

و 6 = ( 94.087 – 92) / 2 = 1.0435

الشكل رقم 4

30º.- f7 . من خلال التفكير المماثل للسابق ، سيكون لدينا:

الأول) x´ = V * p + y * y

x´ = V 81.894×81.894 + 48.5×48.5 = 95.178

الثالث) f7 = (x´ – D) / 2

و 6 = ( 95،178-92) / 2 = 1589

من الممكن إعداد أو الحصول على برنامج كمبيوتر صغير لحساب كل هذه القيم دون الحاجة إلى العمل باليد.

العودة إلى عملية عالم العلب